√99以上 cos(θ π/2)=-sinθ なぜ 218274

 sin(π/2θ)=cosθ cos(π/2θ)=sinθ tann(π/2θ)=1/tanθ の部分（網掛けになっている）が、彼は丁寧にマーカーで塗っているので、目に飛び込みました。 「この部分を全部覚えたの？0以上 cos(θ π/2)=sinθ なぜ Cos(θπ/2)=sinθ なぜ エクセルで cos の値が 05 になる θ を 度 で求める式は =degrees(acos(05)) で結果は ;ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる： sin ⁡ θ = ± 1 − cos 2 ⁡ θ {\displaystyle \sinPolar Coordinates (r,θ) Polar Coordinates (r,θ) in the plane are described by r = distance from the origin and θ ∈ 0,2π) is the counterclockwise angle1 sinθ= cos(π/2θ) 2 cosθ= sin(π/2θ) 3 tanθ= cot(π/2θ) 4 cotθ= tan(π/2θ) 5 secθ= csc(π/2θ) 6 cscθ= sec(π/2θ) =cos π/4 ∵ cos(2nπθ)= cosθ , n ∈ N =1/√2 (xiv) sin (151π/6) Solution sin (151π/6) = sin (25ππ/6)

振動と波動の準備 三角関数の復習 定義と微分 三角関数は 物理でよく使います Ppt Download

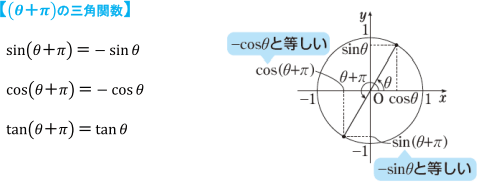
Cos(θ π/2)=-sinθ なぜ

Cos(θ π/2)=-sinθ なぜ-Sin,cosの和と積の関係は、 ( sinθcosθ )を2乗することで求めることができます。 ( sinθcosθ ) 2 = sin 2 2sinθcosθ cos 2 ここで sin 2 θ cos 2 θ=1 という公式が当てはめられることがわかりますね すると、 ( sinθcosθ ) 2 =1 2sinθcosθ 和の2乗=12×積 となり和の2乗倍角，三倍角，半角の公式 加法定理から導出できる三角関数のいろいろな公式です。 毎回導出してもよいですし，時短のために覚えてもよい公式です。 倍角の公式： sin ⁡ 2 x = 2 sin ⁡ x cos ⁡ x \sin 2x=2\sin x\cos x sin2x = 2sinxcosx cos ⁡ 2 x = 2 cos ⁡ 2 x − 1 = 1

大学受験で役立つ加法定理の証明と覚え方を解説 公式を使いこなす Studyplus スタディプラス

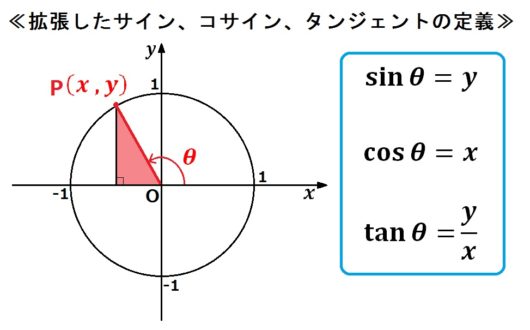
 どうも！地頭コーチSHUです！ 今日も入試数学の解説をしていこうと思います。 今回取り扱うのは 「加法定理の証明」 です。 出題はなんと東京大学！1999年の入試で理系文系ともにF (r, θ)=0 などの形で表したものを極方程式といいます． 例1 原点を中心とする半径 a (>0) （一定） の円の極方程式は r=a で表されます． この極方程式には，見かけ上 θ が書かれていませんが，それは任意の θ の値に対して （どんな θ の値に対して点を動かしながら、それぞれの辺の比（sin,cos,tan）がどういう量かを実感しよう。 sinθ= cosθ= tanθ= 次のページへ 三角関数を図解する その2：θの範囲について 前のページで遊んでみた人は、θという角度が0からπ/2という範囲以外にもなることに気づいただろうか？ 発見できる人には自分で発見して欲しいと思って、あえて説明していなかったが、点は元々の三角

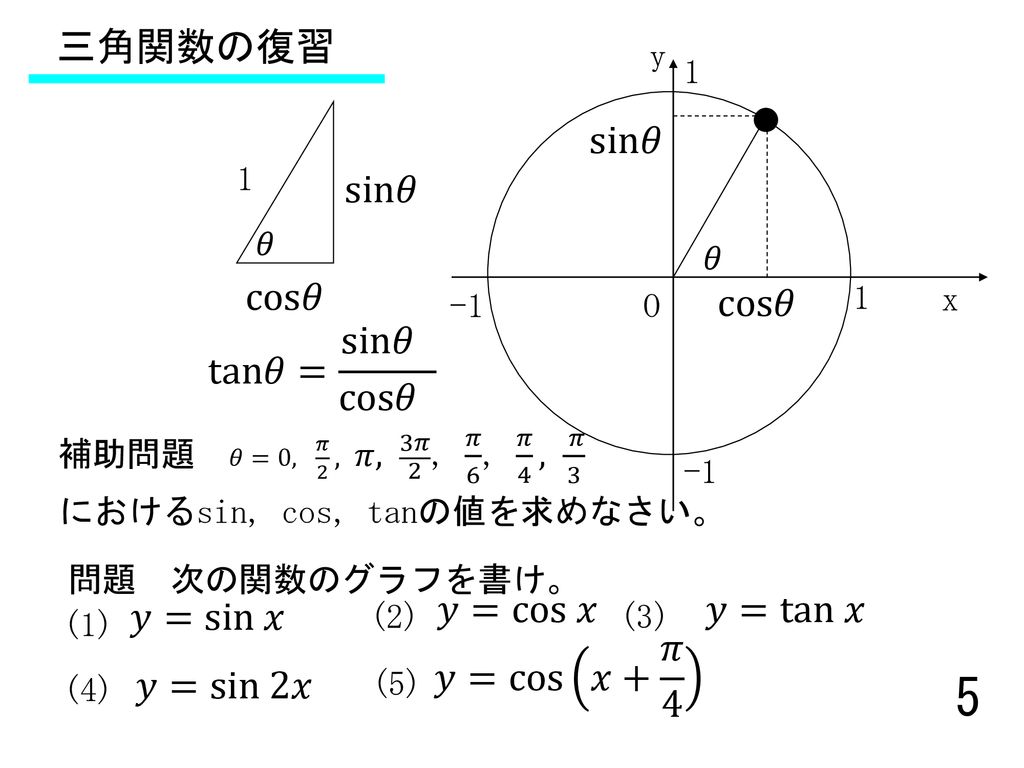
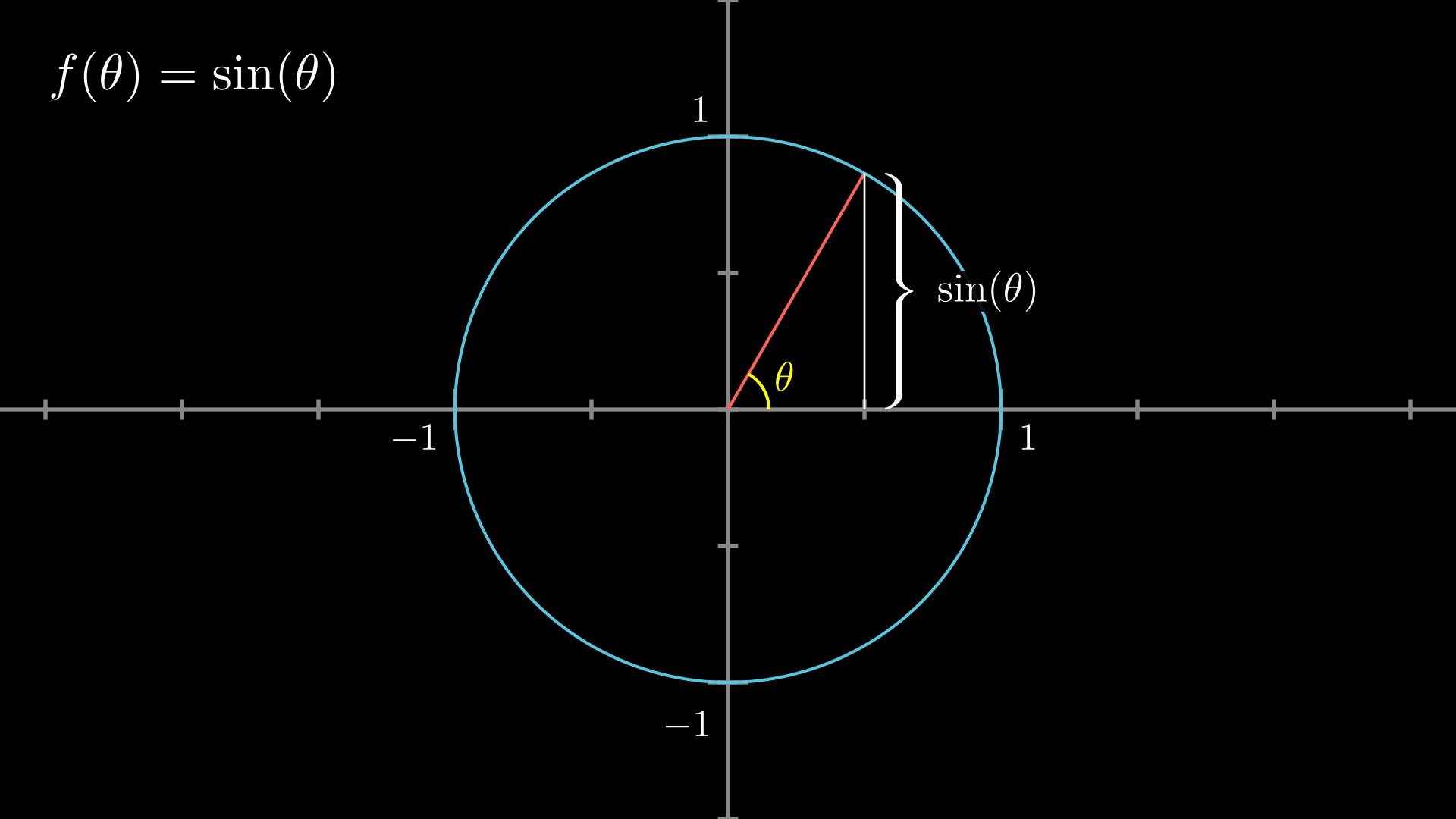
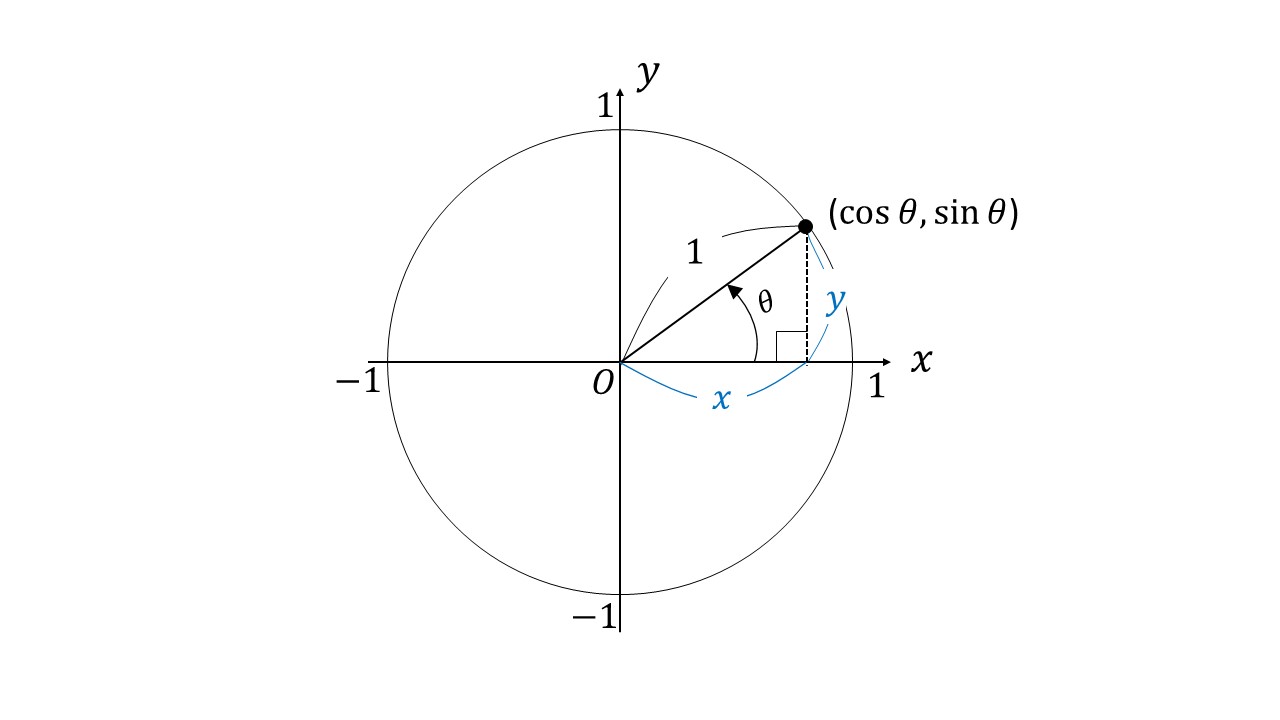
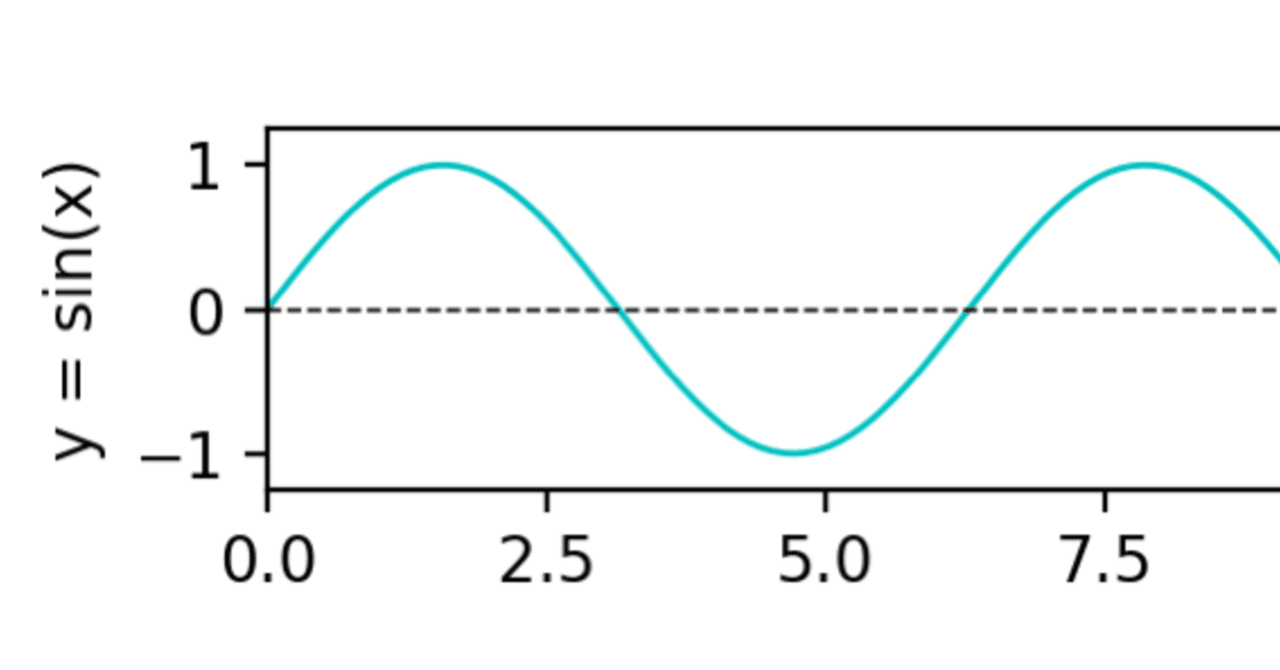
三角比の中でも、 sinθ, cosθ (θ = 0, π / 6, π / 4, π / 3, π / 2) の値はよく使うので、できれば完璧に暗記しておきたいところ。 sinθ と cosθ は √a 2 の形で覚えると暗記しやすいですよ。 2π / 3 ≦ θ ≦ 2π における三角比も見ていくと、こんな感じ。 こちらは 「 θ = 0, π / 6, π / 4, π / 3, π / 2 」 の表を覚えておけば後述の公式から求められるので、絶対に暗記しないと sin(θπ/2)=cosθ は、暗記できるならしても良いですが、 加法定理でいつでも導けるので、忘れても大丈夫と私は思っています。 sin(θπ/2)=sinθcos(π/2) cosθsin(π/2) = sinθ*0 cosθ*1 = cosθ 今回の問題は、以下の方法で解いてみました。(sinθとcosθの関係から出せることを忘れていたので) sin を cosにし（1） y=sinθ のグラフ 第2図を見てください。Pの y 座標が sinθ の値になることが分かるはずである。 したがって、横軸に θ の値をとり、縦軸に各 θ に対する sinθ の値を目盛ってグラフを書くと第3図のようになる。 書き方は例えば、右の θ 軸上 θ=π/6 で、 θ 軸に立てた垂線と、 θ=π/6 に

三角関数の合成公式の証明と応用 レベル ★ 基礎 三角比・三角関数 更新日時 三角関数の合成公式 とは，sin と cos が混ざった式を，sin だけで表すための，以下のような公式です。 a sin ⁡ θ b cos ⁡ θ = a 2 b 2 sin ⁡ ( θ α) a\sin\thetab\cos\thetaCos ⁡ (θ π / 2) = − sin ⁡ θ と sin ⁡ (θ π / 2) = cos ⁡ θ は式（加法定理を使うだけです）よりも，単位円などを描いて図で理解した方が分かりやすく間違えにくいと思います． よって、 ①式のdl,rをθに変換し、変数をθのみにします。 変数をθのみにしたら①式を積分して直線電流の磁界Hを求めます。 rをθに変換する a/r=cos(θπ/2)=sinθ r=a/sinθ・・・② となりθに変換できました。 dlをθに変換する

回転行列 なんでマイナスが右上に

3

 この問題がわかりません。 出来れば途中の式など詳しく教えて欲しいです。 C1x=1cosθ、y=θsinθ(0≦θ≦π) C2y=3k(xa)^2/3 (x≧a) C1は半径1の円がy軸に接しながら 滑ることなく回転するサイクロイドの一部。 C1,C2は点(1, (π/2)1)を共有し、ここで共通接線を持つ。 cosθ とした時の地域を間違えました −√3/2≦θ≦1 1≦cosθ≦1 になります。 問が sinθ なので θ=0の時、sinθ=0 θ＝π/2の時 sinθ=1 θ=4π/3の時 sinθ=1/2 1/2≦sinθ≦1 になりますね。 3各定規に関係する角度のπ/6やπ/4の倍数の時、sinθ、cosθ、tanθがどういう値を取るか、 (2)について dS/dθ＝sin2θcos2θ/2 －1/2という値が出てきますが、ここから三角関数をcosで合成する方針で問題を解いて欲しいです。 理解力がないので出来れば詳しく書いて欲しいで

三角関数 って 何でしたっけ Sin サイン Cos コサイン Tan タンジェント ニッセイ基礎研究所

Sin P 2 8 の考え方がわかりません 僕なりの考え方はsin P Yahoo 知恵袋

加法定理の応用 テスト勉強中に分からない問題がでてきて困っています； 加法定理の応用(2倍角、半角)の問題で 「π/2＜θ＜π , sinθ＝2/3のとき sin2θ , cos2θ , tanθ/2の値を求めよ」 というものなのでそして結論から言うと、タイトルの通り sin の微分は cos になります。 それでは、なぜそうなるのでしょうか？ (θ)の長さは、θの値が 0 から π（180度）の間は正の値になり、π（180度）から 2π（360度）の間は負の値になります。 2 sinの微分はcosと書けることになります． しかし，一般には asin θbcos θ のように与えられた係数， a, b がそのままで一つの角度 α の三角関数 cos α, sin α に等しいことはめったにありません． 右図のように a, b が2辺となっている直角三角形を考えると，

三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita

なぜsin 8 P 2 Cos8になるのでしょうか Clearnote

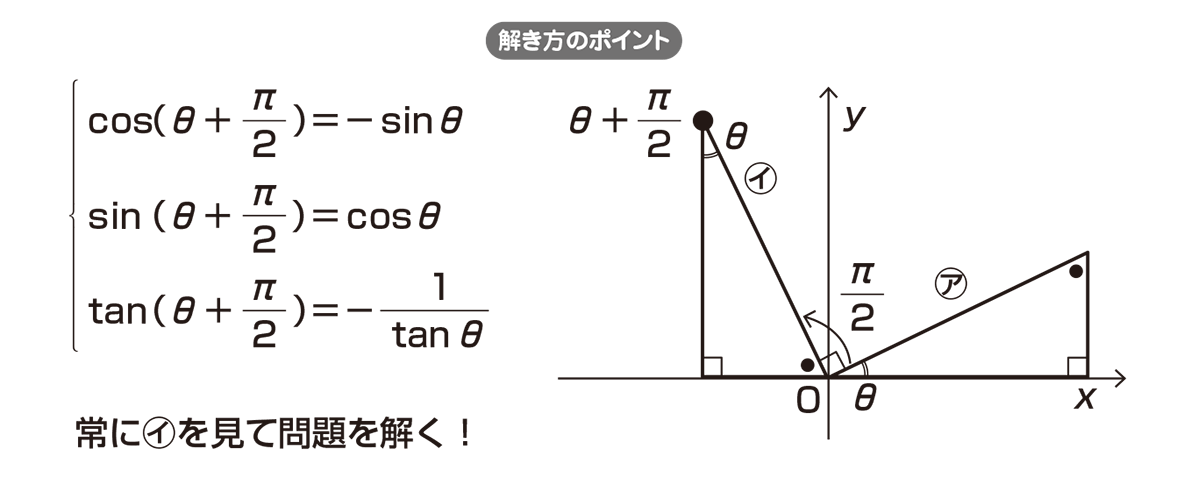
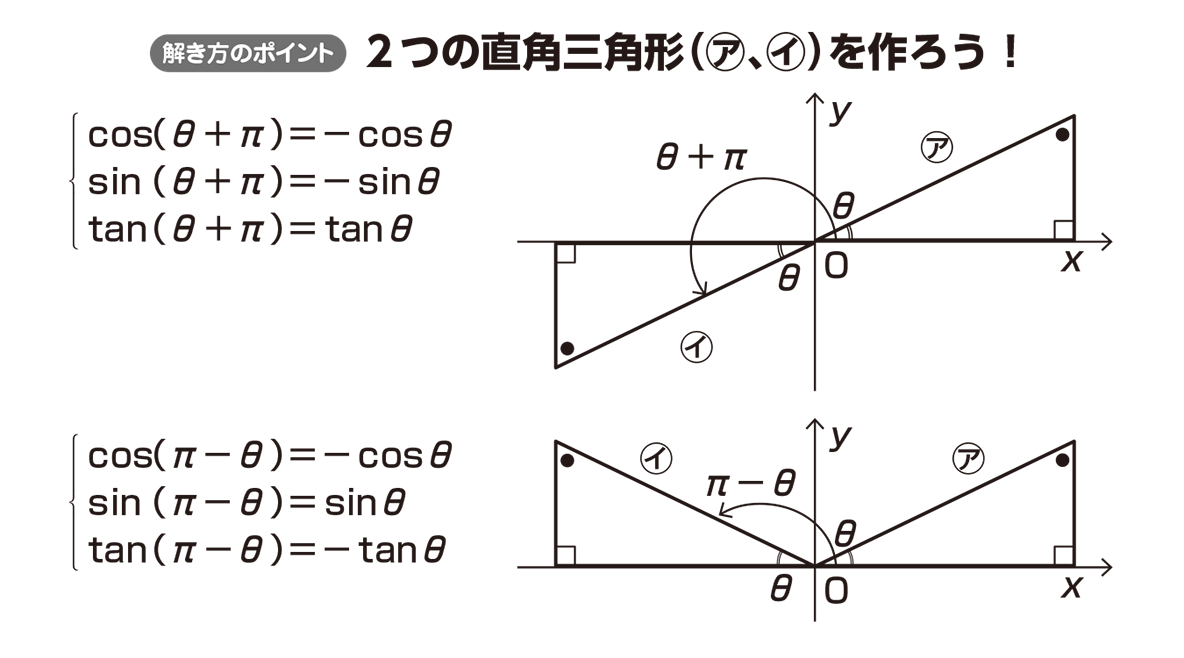
ご質問の分数について，その分母 cos^2 Θ sin^2 Θ は，あの有名な公式の左辺ではないですか？ cos^2 Θ sin^2 Θ ＝ 1 つまり分母は1ですので，その分数は分子と一致していますよ！ これで分かり符号にも注意を！ では、直角三角形イで (θπ/2)の三角比を考えましょう。 「底辺」と「高さ」が入れ替わっているので、 cos (θπ/2)=sinθ sin (θπ/2)=cosθ tan (θπ/2)=1/tanθ と表せます。 符号の変化にも注意してください。 では、ポイントを使って実際に問題を解いてみましょう。このsinθ 、cosθ 、tanθを角θの三角関数といいます。 三角関数の性質 一般角の三角関数についても、数学Iの三角比と同じような相互関係が成り立ちます。 \(・sin^2 θcos^2 θ=1\) \(・tanθ=\frac{sinθ}{cosθ}\) \(・1tan^2 θ=\frac{1}{(cos^2 θ)}\) 三角関数のグラフ

三角関数の性質 8 P 2の角の公式の証明 数学ii By ふぇるまー マナペディア

Sin 8 P 2 や90 8など還元公式の覚え方の解説 余角 補角の攻略

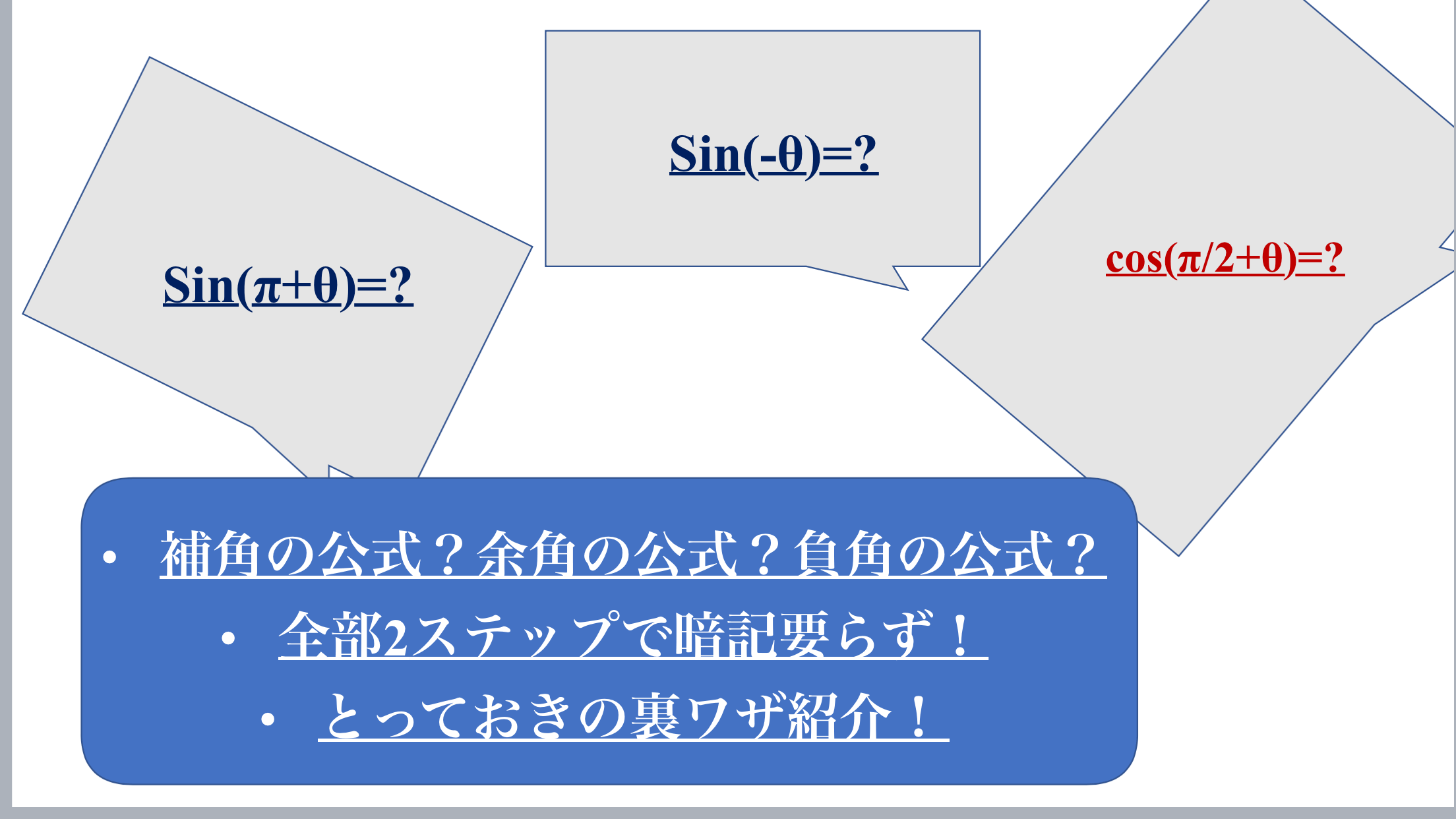
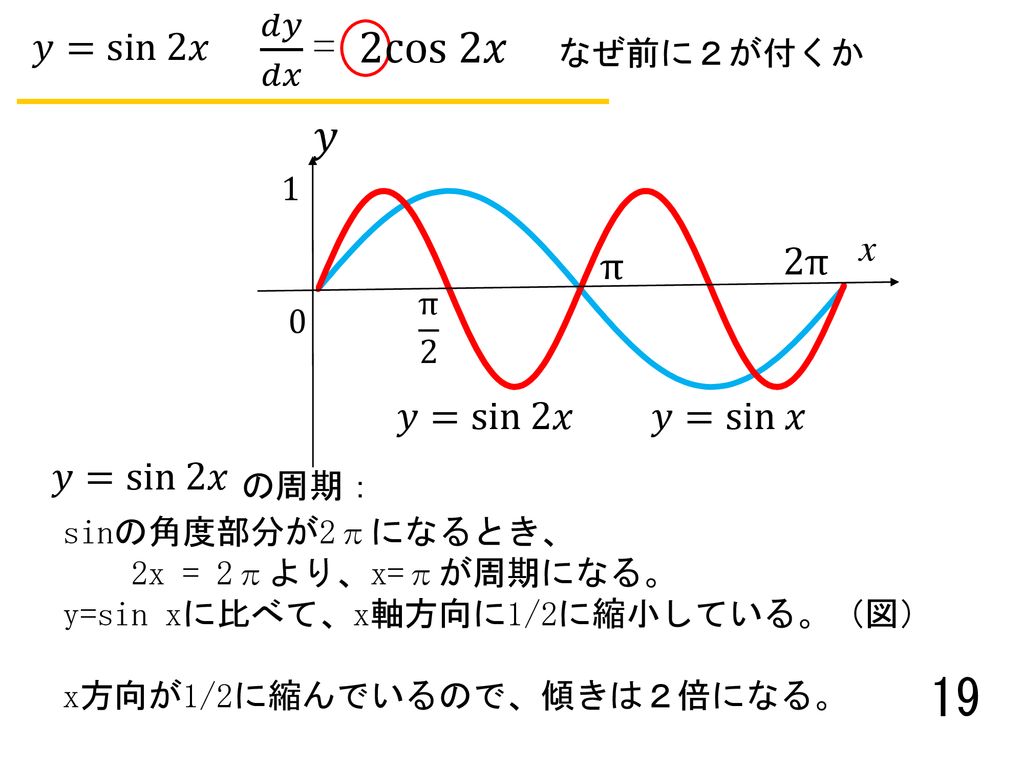
 なぜこうなるのかがわからないです。 わかる方教えてほしいです🙇‍♀️ sin2x のグラフをぇ軸方向へ ? さあ「sinθ」と「θ」の基本的かつ重要な性質が分かったところで、この2つを結びつけていこう。 ところでこの近似「sinθ ≒ θ」には、 重要な前提条件 がある。 それは、 θがものすごく小さい ということだ。 θ が 1°とか 2° とか、そういうときは使えるって感じで、θが小さければ小さい 三角関数の性質の、 sin(θπ)=sinθや、 cos(θπ/2)=sinθ、 tan(θ)＝tanθなどは、どうしてそうなるんですか？ 全部暗記しなくてはならないんでしょうか？

Sinの微分はなぜcos 誰でも直観的に理解できるように解説 Headboost

半角公式が一目でわかる 証明 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ

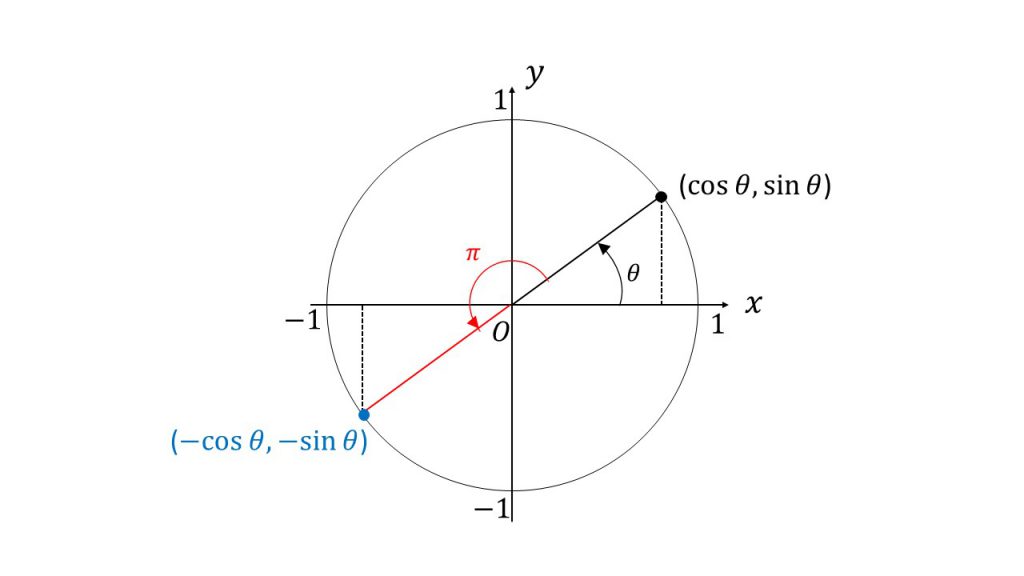
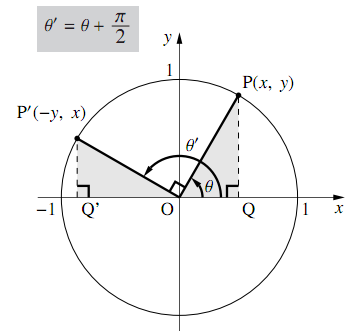
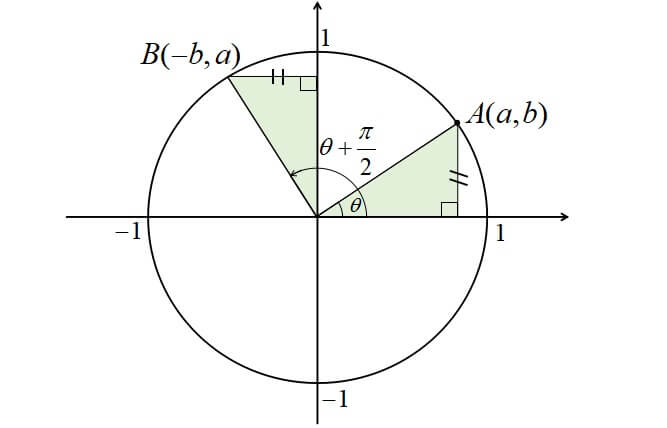
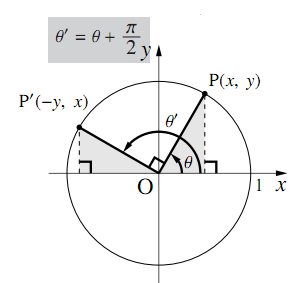
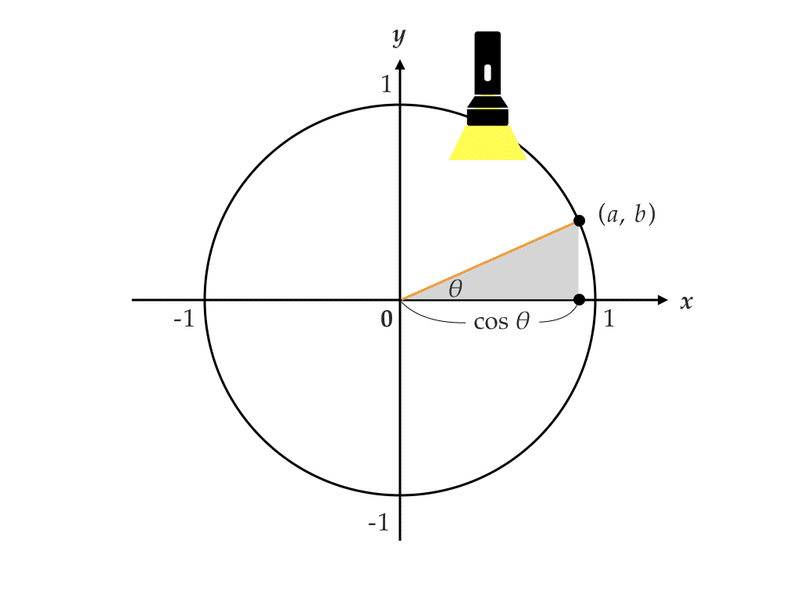
 すると、θのときの直角三角形と、π/2－θの直角三角形は合同なので、縦の長さが赤となり、横の長さが青となります。 よってこの点のx座標は青つまりsinθとなり、この点のy座標は赤つまりcosθとなります。 ゆえに、 sin (π/2－θ)=cosθとなり、 cos (π/2－θ)=sinθとなり、 tan (π/2－θ)=sin (π/2－θ)/cos (π/2－θ)=cosθ/sinθ=1/tanθとなります 」 ⑧「同様にして（ⅵ）ピタゴラスの定理 や オイラーの公式 などから以下の基本的な関係が導ける 。 cos 2 ⁡ θ sin 2 ⁡ θ = 1 {\displaystyle \cos ^ {2}\theta \sin ^ {2}\theta =1\!} ここで sin2 θ は (sin (θ))2 を意味する。 この式を変形して、以下の式が導かれる： sin ⁡ θ = ± 1 − cos 2 ⁡ θ {\displaystyle \sin \theta =\pm {\sqrt {1\cos ^ {2}\theta }}}だけ, 了軸方向へちあだけ平行移動したら, ーーcos 2み人 ) 2のクラフと一致した。 定数 @。 のの値を求めよ。ただし, 0Sミez とする。 8 を タニ ーcos

Return 8 0 のとき Sin8 8 1 という公式の証明

数学 Sina Cos P 2 A なぜこのような式になるのでし Okwave

レベル ★ 基礎 三角比・三角関数 更新日時 sin ⁡ x \sin x sinx および cos ⁡ x \cos x cosx は微分すると位相が90度進む。 積分すると位相が90度遅れる。 三角関数の微分・積分と位相の進み・遅れについて紹介します。 解答3：相互関係&因数分解の利用 （解説3）条件の不等式は、2cos 2 sin 2 θcos 2 θ＝1（相互関係）を使って次数の低いsinθに合わせます。 その後、たすき掛けをして＜参考：「因数分解の解き方と工夫まとめ」＞不等式を解いていきます。 2cos 2 不等号の向き三角関数の角度を求める公式と計算 三角関数の角度を求める公式を下記に示します。 それぞれ「アークサイン」「アークコサイン」「アークタンジェント」といいます。 下式のyの値が同じでもSin、cos、tanごとに角度θの値は変わります。 三角関数の

オイラーの公式が人類の至宝と呼ばれる理由 8 P 半円マジック虚から出た宇宙の真理 発想力教育研究所 素数誕生のメカニズム

三角関数の性質を単位円で理解する 8 2ｎp 8 P 8 P 2 8 大学受験の王道

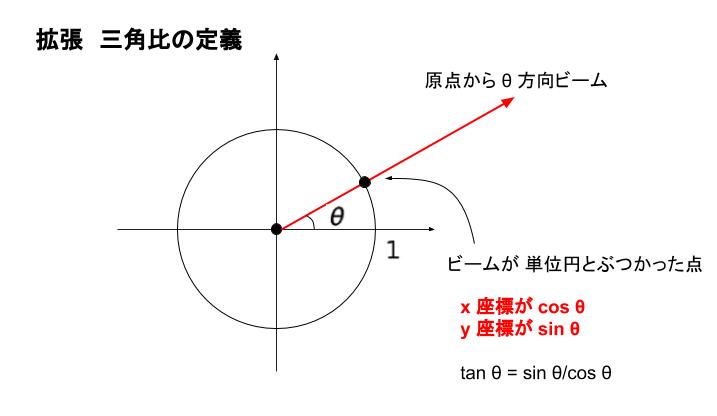
三角関数というのは「角度→直角三角形の辺の比」という関数としてまず定義される。 つまり、「直角三角形の角度を一つ決めると、辺の比が決まる」という関係が「三角関数」である。 理工学では、角度は「度」ではなく一周を 2 π 2\pi 2π とする角度がよく使われることが多い なぜか、というのはこの後三角関数の性質を考えていくなかで理解できるはずである 数学 高校生 3年弱前 ｿ ﾌ ｨ ｱ cos (π/2θ)はなぜSinθなのですか？ ？

Sin ２分の３p 8 が Cos8 になるのはどうしてですか Clearnote

センター試験をやってみた Part 3 数 B その2 Fire Wings

高校数学 8 と 8 P 2 の関係 映像授業のtry It トライイット

振動と波動の準備 三角関数の復習 定義と微分 三角関数は 物理でよく使います Ppt Download

置換積分はなぜ置換するのか コツは2つのタイプを区別すること ラディカル高校数学

ド文系が 三角比の拡張 と ラジアン をわかりやすく解説する

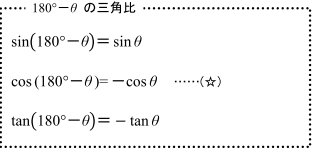
180 8の三角比 数学 苦手解決q A 進研ゼミ高校講座

三角関数の性質を単位円で理解する 8 2ｎp 8 P 8 P 2 8 大学受験の王道

複素数平面 複素数の極形式 数学 定期テスト対策サイト

マーカーのところはなぜ P 6 8 P 4 5p 6 ではないのでしょうか Clearnote

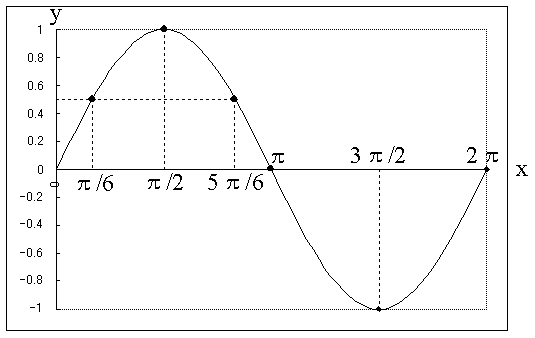
三角関数

極方程式の面積 扇形積分 おいしい数学

2

8 P 2の三角関数 数学ii フリー教材開発コミュニティ Ftext

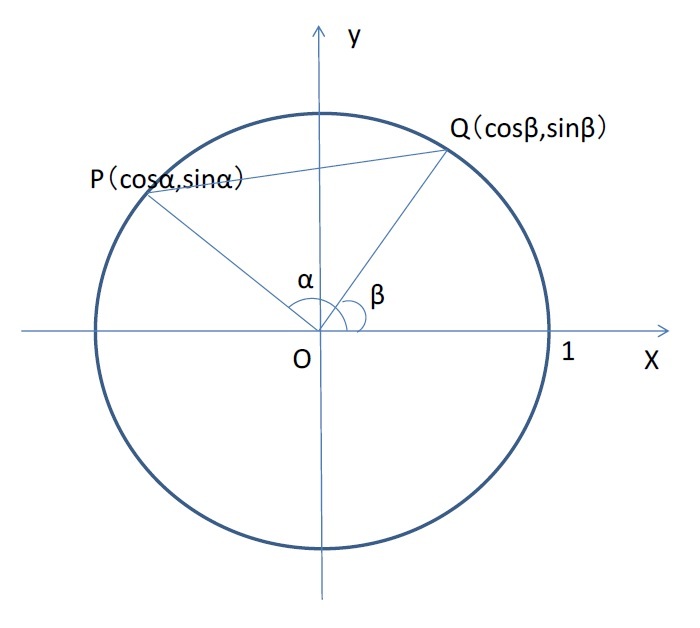
三角関数 の基本的な定理とその有用性を再確認してみませんか その２ 加法定理 二倍角 三倍角 半角の公式等 ニッセイ基礎研究所

三角関数の合成公式 三角関数の公式一覧

16 合成公式はsinだけじゃないんです 医学生gの数学ノート

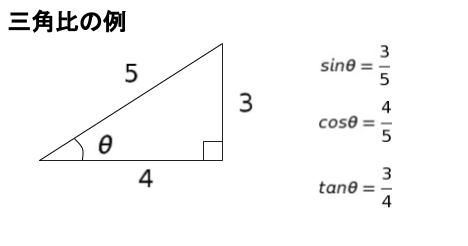
三角形の辺の比による三角関数の定義

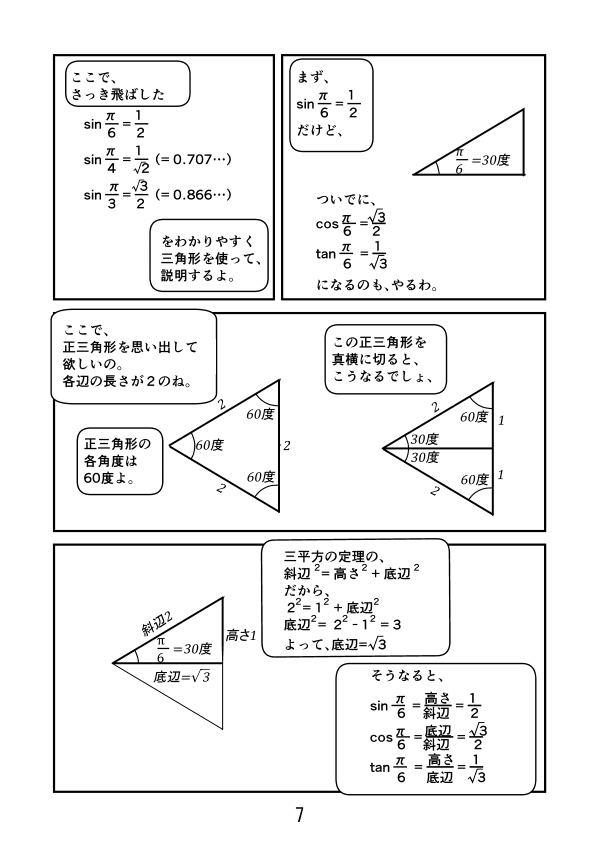
漫画で高校数学 8 P 6 P 4 P 3の時のsin8 Cos8 Tan8の値 三角関数22 Manabi100

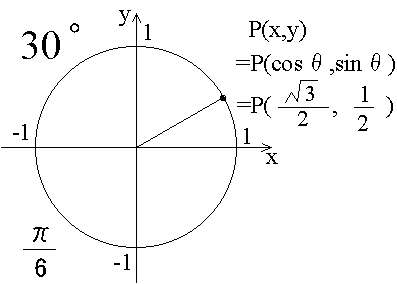
三角関数

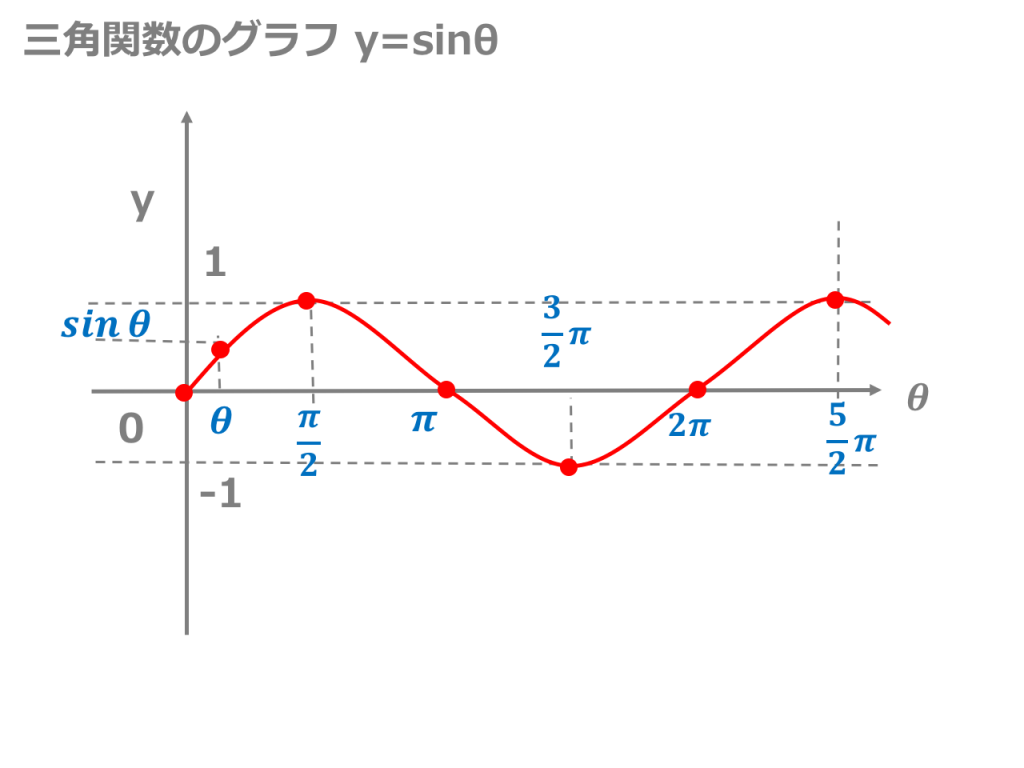
3分でわかる 三角関数のグラフの描き方 合格サプリ

二次方程式の解と係数の関係が成り立つ仕組みをおさらい 解が三角関数のとき 東京都立大17文系第1問 Mm参考書

三角関数についてです 写真の 2 についてなのですが なぜt P 4なの 数学 教えて Goo

Cos 8 P 2 Sin8 Sin 8 P 2 Cos8 Cos 8 P 2 Sin8 S Cos 8 P 2 S 数学 教えて Goo

どうして三角関数で度数法じゃなくて弧度法を使うの シャンのいろいろ2

1

大学受験で役立つ加法定理の証明と覚え方を解説 公式を使いこなす Studyplus スタディプラス

標準 三角関数のグラフ なかけんの数学ノート

三角関数 合成はやり方と目的さえわかれば克服できます 大学受験数学の解き方

Y Cos 28 P 2 のグラフの書き方 三角関数のグラフ 数学ii By ふぇるまー マナペディア

なぜdh法の同次変換行列の積は左にかけていかないのか 定性的な解釈を考える 同次変換行列の勉強

ド文系が 三角比の拡張 と ラジアン をわかりやすく解説する

三角関数の合成 おいしい数学

三角比 三角関数の公式を単位円と関連づけて理解する 関谷 翔 Note

8 P 2 8 P三角関数の公式と導き方

センター試験年度 数ia 第２問 １ １ 三角関数 サンディエゴ駐在者による現地生活紹介と文系のための数学

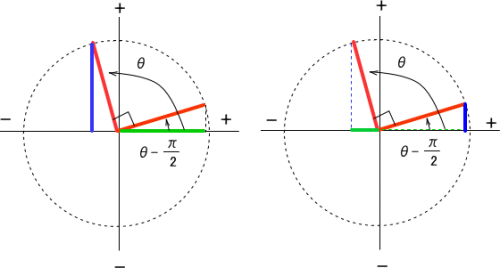
Cos 8 P 2 Sin8 Sin 8 P 2 Cos8 になるんですか Cos 8 P 2 Sin8 数学 教えて Goo

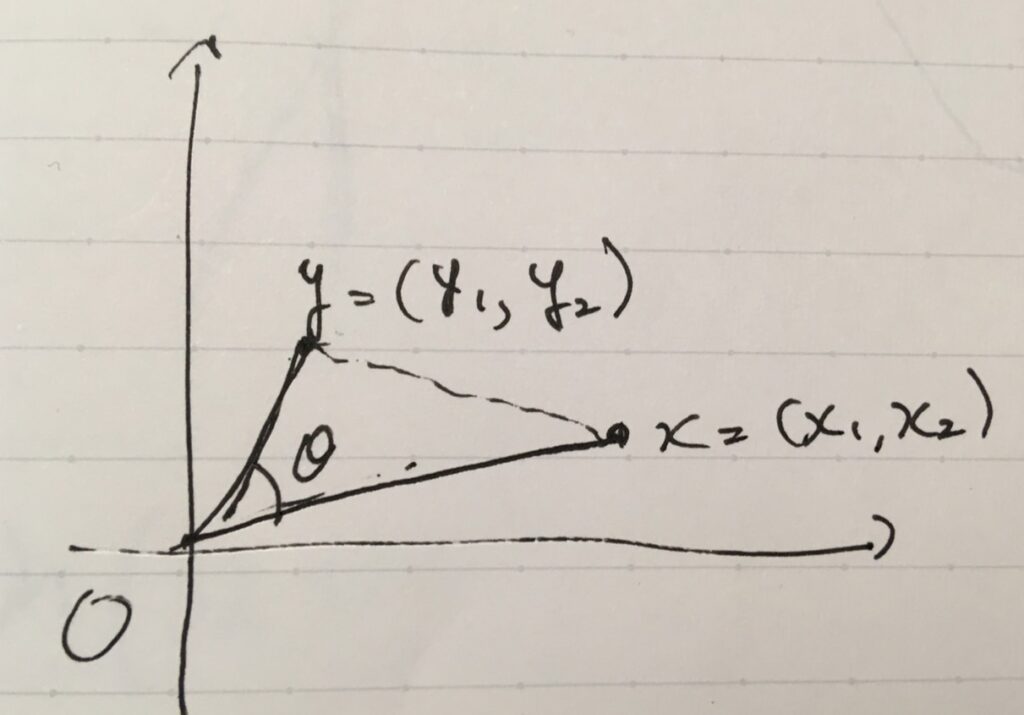
余弦定理とベクトルの内積の関係 なぜコサインか 趣味の大学数学

高校数学 単位円を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 0 180 の三角比 受験の月

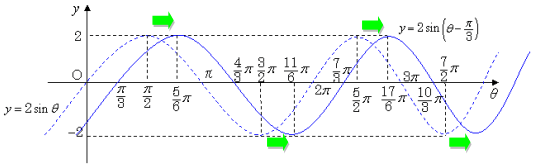
複雑な三角関数のグラフ 数学 苦手解決q A 進研ゼミ高校講座

1

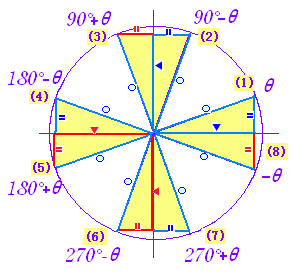
数２ 三角関数 性質

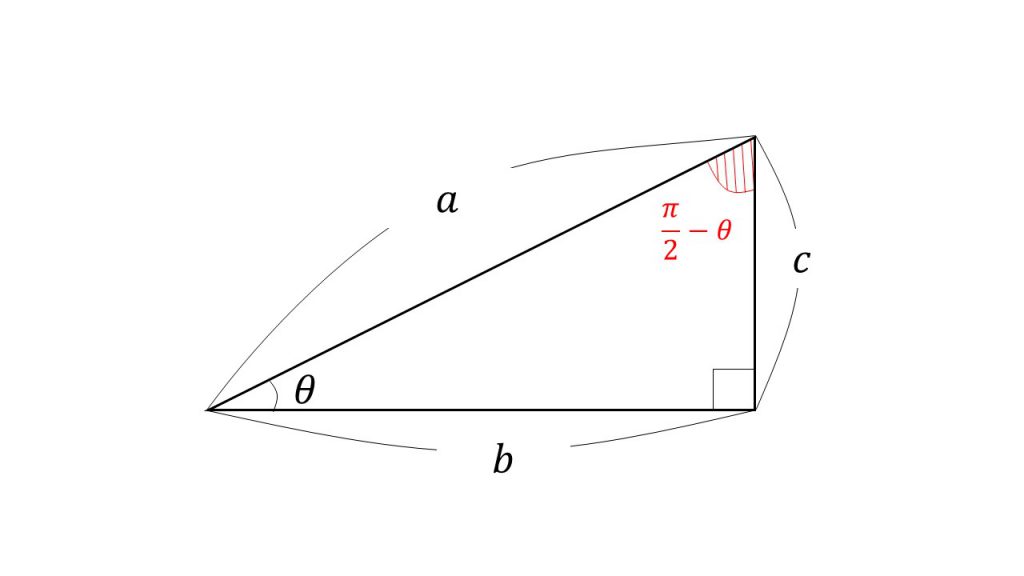
三角関数の性質を単位円で理解する 8 2ｎp 8 P 8 P 2 8 大学受験の王道

Cos P 2 8 はなぜ Sin8なのですか Clearnote

三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ

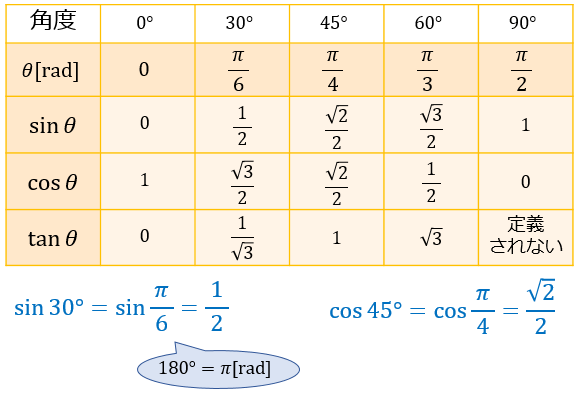
三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ

三角関数 薬学 これでok

三角関数 どうしてsin P 2 8 がcos8になるんです Yahoo 知恵袋

8 2np 8 8 P 8 P 2 P 8 P 2 8の三角関数 数学ii 三角関数 7 Youtube

8 P 2の三角関数 数学ii フリー教材開発コミュニティ Ftext

三角関数 どうしてsin P 2 8 がcos8になるんです Yahoo 知恵袋

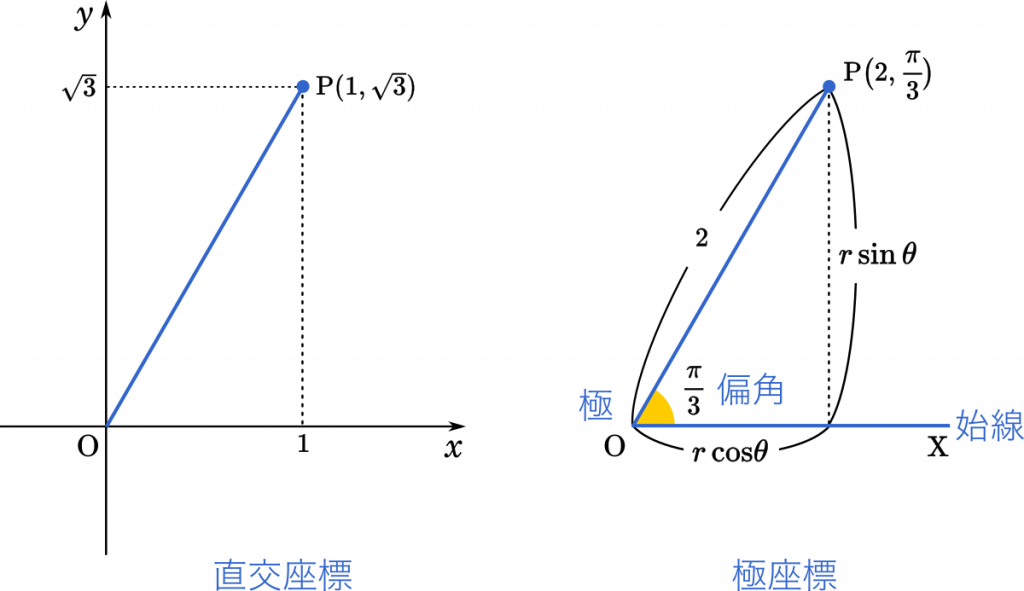
数iii極座標 極方程式 極方程式の授業を聞いてなかったのでおさらいする Mm参考書

Arccos0の値ってなぜp 2なんですか Arccos0の値ってなぜp 2なんで 数学 教えて Goo

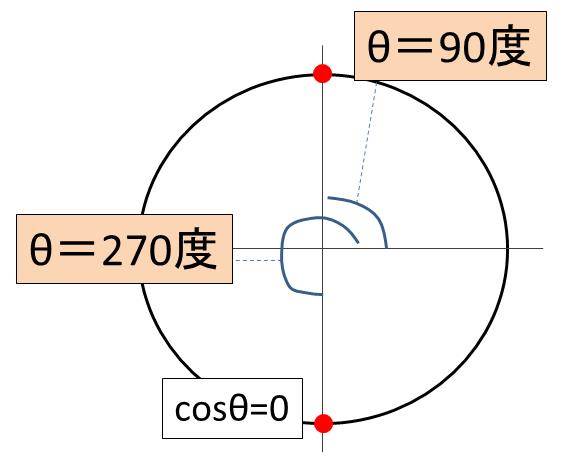
Cos8 0 やcos8 1の角度 8の値 は何度か Sin8 0 やsin8 1の角度 8の値 は 単位円 ウルトラフリーダム

Sin 8 2分のp がcos8になる理由がわからないのだか Yahoo 知恵袋

1 Cos8 1の時8 0になるのはなぜですか 2 Cos8 0で2ぶんのp 高校 教えて Goo

Y Sin 28 P 2 のグラフの書き方 三角関数のグラフ 数学ii By ふぇるまー マナペディア

三角関数 合成はやり方と目的さえわかれば克服できます 大学受験数学の解き方

逆三角関数をなぜ学ぶか その微分と積分計算への応用 趣味の大学数学

漫画で高校数学 8 P 6 P 4 P 3の時のsin8 Cos8 Tan8の値 三角関数22 Manabi100

磁界 H I 2pa を求めてみました 理論 ノリユキのブログ

高校数学 8 と 8 P 2 の関係 映像授業のtry It トライイット

小さい角度のsinとtan

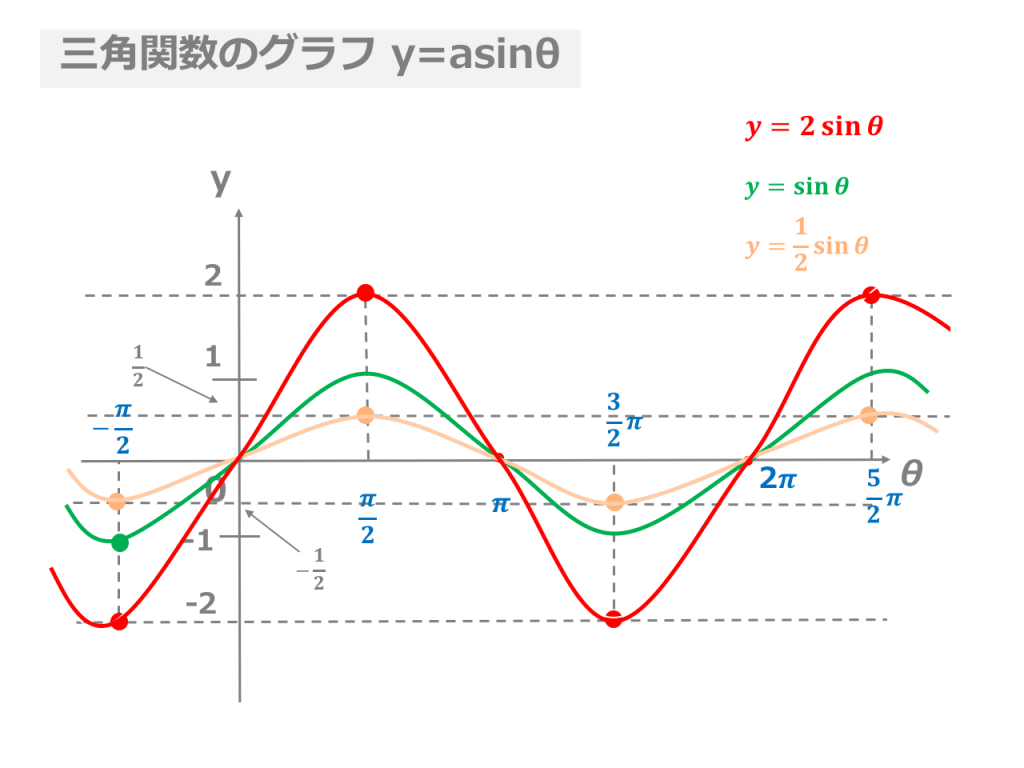
3分でわかる 三角関数のグラフの描き方 合格サプリ

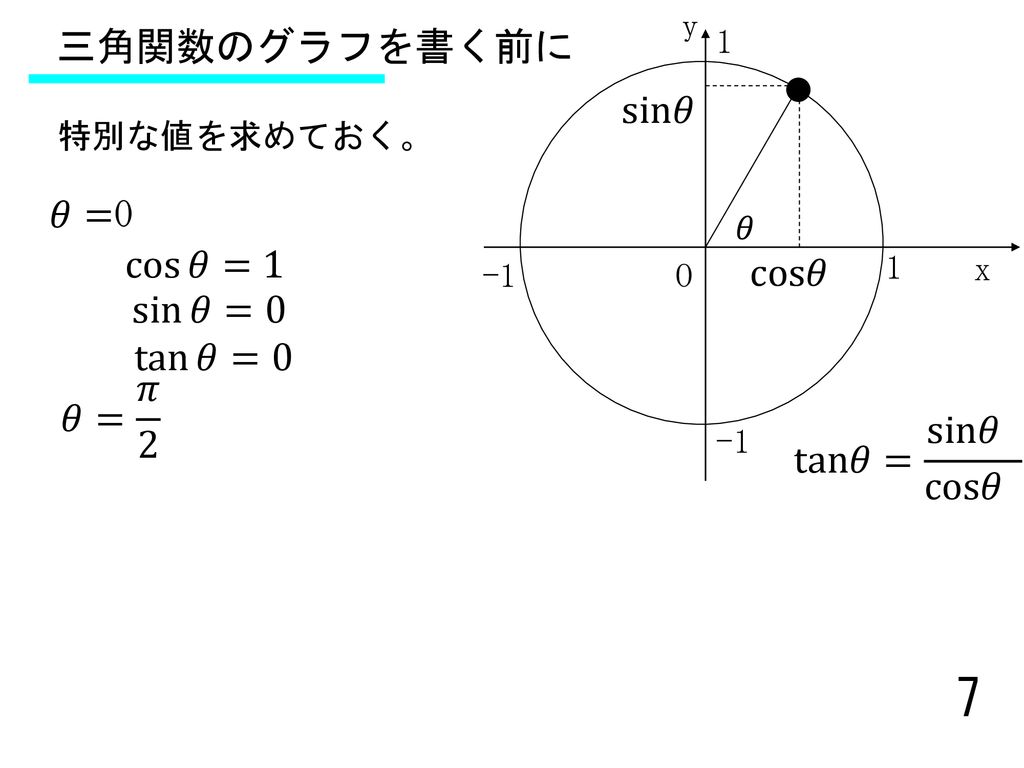
振動と波動の準備 三角関数の復習 定義と微分 三角関数は 物理でよく使います Ppt Download

数学 Sina Cos P 2 A なぜこのような式になるのでし Okwave

振動と波動の準備 三角関数の復習 定義と微分 三角関数は 物理でよく使います Ppt Download

Sinの微分はなぜcos 誰でも直観的に理解できるように解説 Headboost

三角関数では Cos8 Sin P 2 8 と書くことが出来て Tan8 Sin8 Cos8 Sin8 Sin P 2 8 として表すことが出来るのに なぜcos8 Tan8が必要でしょうか Quora

高校数学 8 と 8 P 8 Pの関係 映像授業のtry It トライイット

三角形の辺の比による三角関数の定義

三角関数 薬学 これでok

Sin 8 P 2 Cos8

標準 三角関数のグラフ なかけんの数学ノート

三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ

嶋内 Tan 8 2分のp がマイナスtan8分の1になる理由を教えていただきたいです 内が なので Tan8分の1では無いのですか Tan Pー8 はtan8になるのでそう思いました 数学 数学教えて 受験

2

先程答えてくださった人には申し訳ないですが理解できなかったので質問させていた Clearnote

数ii 三角関数の最大 最小 学校で購入した問題集の問題なのですが解説に Okwave

三角比 三角関数の公式を単位円と関連づけて理解する 関谷 翔 Note

Sin 8 P 2 や90 8など還元公式の覚え方の解説 余角 補角の攻略

三角関数の公式覚え方sin Cos Tan M君

三角関数についてですが Tan 8 P 2 1 Tan8となる理由を教えて Yahoo 知恵袋

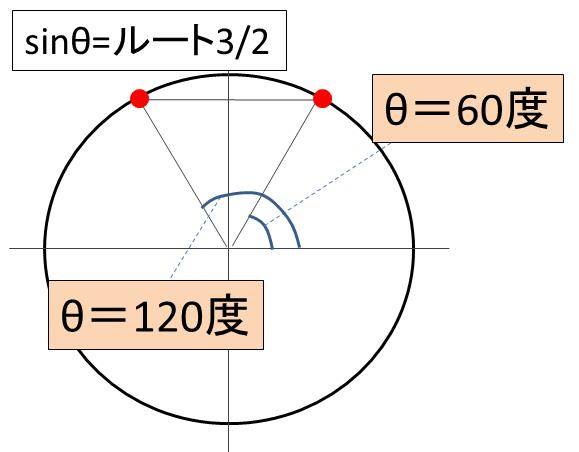
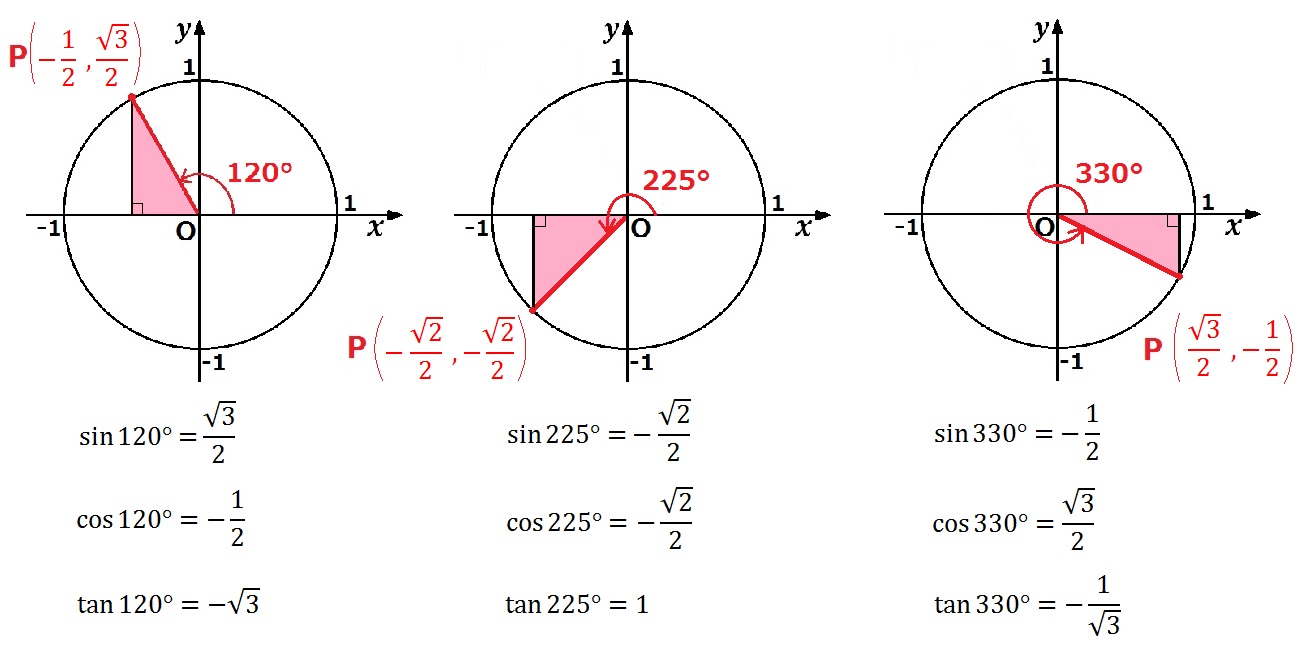
Sin8 1 2の角度 8の値 は Sin8 ルート3 2やsin8 1 ルート2 ルート2分の1 を満たす角度は何度 単位円 ウルトラフリーダム

三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ

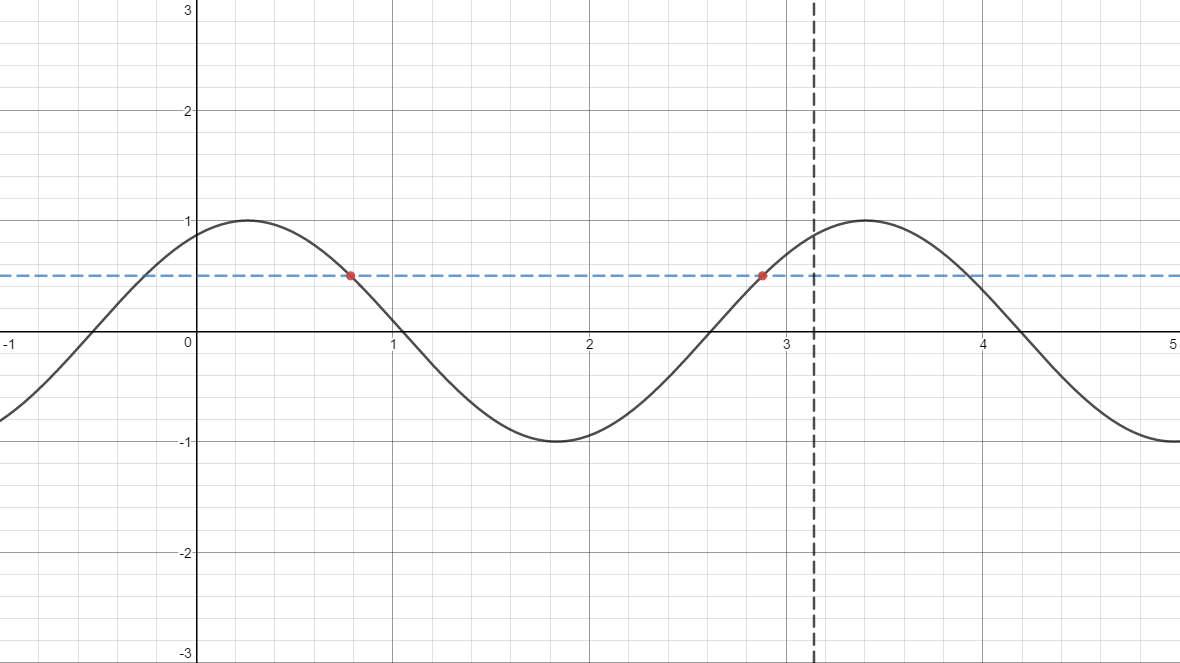
Question Ac026 Socratic

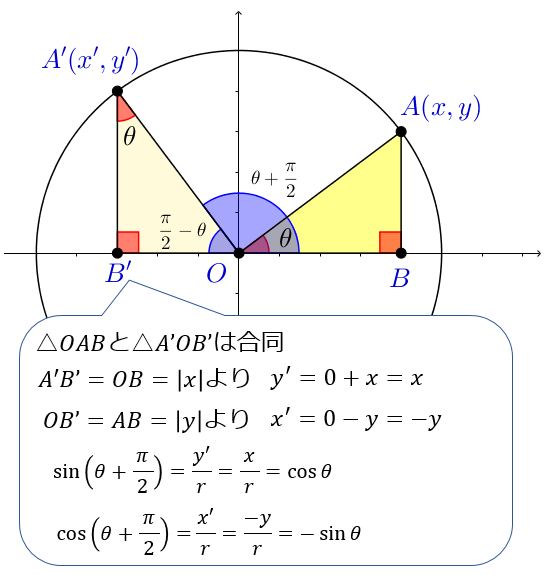
三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ

半角公式が一目でわかる 証明 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ

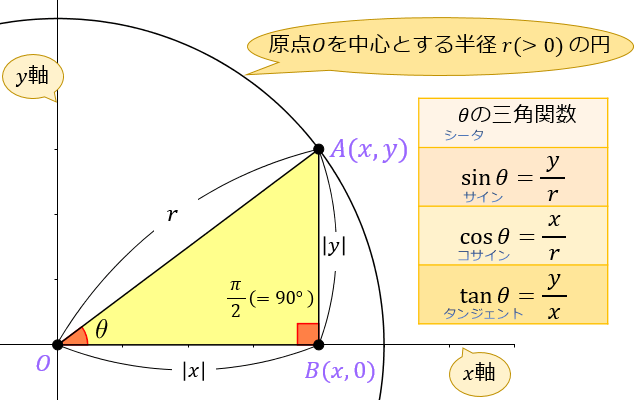
三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ

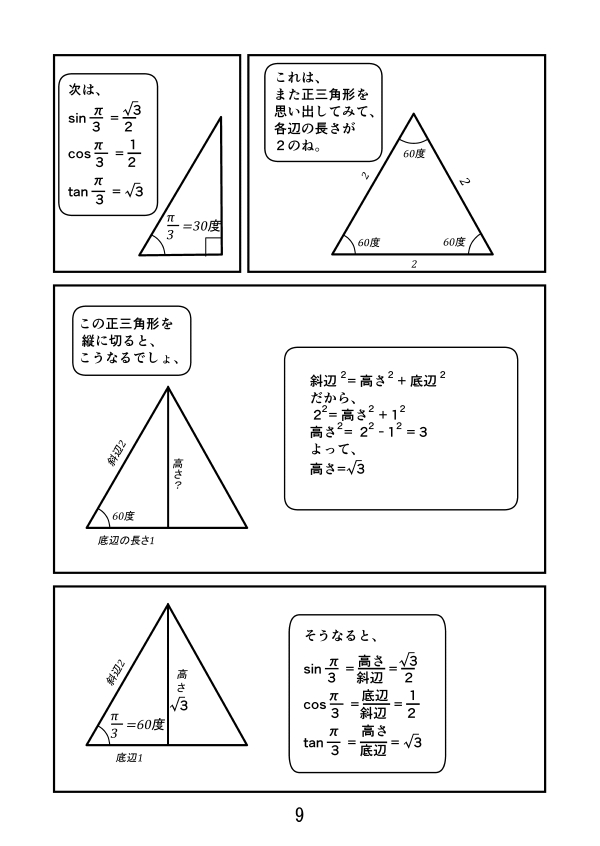
漫画で高校数学 8 P 6 P 4 P 3の時のsin8 Cos8 Tan8の値 三角関数22 Manabi100