Share It On Facebook Twitter Email 1 Answer 1 vote answered by Sarita01 (535k points) selected byCos2x=1tan^2x/1tan^2x1tan^2x/1tan^2x is equal toShow that cos 2x = 1 tan^2x/1 tan^2xprove that cos2x=(1tan^2x)/(1tan^2x) #math , #trigonometry , # cos2x=1tan^2x/1tan^2x1tan^2x/1 Click here 👆 to get an answer to your question ️ prove that 1sin2x/1sin2x=tan^2(pi/4x)

Tan2x ただの悪魔の画像
Prove that cos2x=1-tan^2x/1 tan^2x
Prove that cos2x=1-tan^2x/1 tan^2x- In this way (remembering that tanx=sinx/cosx and sin^2xcos^2x=1), the second member becomes (1sin^2x/cos^2x)/(1sin^2x/cos^2x)=((cos^2xsin^2x)/cos^2x)/((cos^2xsin^2x)/cos^2x)= =((cos^2xsin^2x)/cos^2x)*cos^2x/(cos^2xsin^2x)= =cos^2xsin^2x, that is the development of the formula of cos2xGet an answer for 'trigonometry Prove that cos2x(1 tanx*tan2x) = 1' and find homework help for other trigonometry math questions at eNotes This proves that cos 2x * (1 tan x*tan 2x) = 1




Solved Prove That The Equations Are Identities 1 Chegg Com
To Prove that tan − 1 (1 3 ⋅ tan x) = 1 2 ⋅ cos − 1 (1 2 cos 2 x 2 cos 2 x) Let tan x = 3 ⋅ tan θ (E01) θ = tan − 1 ( tan x 3 ) Prove that cos2x = {(cos 2 x sin 2 x), (2cos 2 x 1), (1 2sin 2 x), ((1 tan 2 x)/(1 tan 2 x)) trigonometric functions; Prove the identity 1 (sin^2 x/(1 cot x)) (cos^2 x/(1 tan x)) = sin x cos x asked in Trigonometry by RahulYadav ( 531k points) trigonometric functions
Hintwrite sin(2x) & tan(2x) in terms of tan(x)orwrite cos(2x) in terms of tan(x)Precalculus Precalculus questions and answers 78 1 cos 2x sin 2x tan x C 2 79 tan () cos x tan sina 2 2 Answer 80 tan C 2 COS X CSC= sin x 2 81 sin 43 = 4 cos x cos 2x sin a Get an answer for 'Show that `tan^2 x = (1 cos(2x))/(1 cos(2x))`' and find homework help for other Math questions at eNotes Prove that `sec^4(x)tan^4(x)=1tan^2(x)` 3 Educator answers
You can put this solution on YOUR website!Answer (1 of 5) Sin 2x = 2 sinx cosx Cos2x = 2 cos^2 x 1 So, (sin 2x)/(1cos 2x) = 2 sin x cos x /(1 2 cos^2 x 1) = 2 sin x cos x /2 cos^2 x = sin x /cos x = tan x For the second part,we have tanx = sin 2x/(1cos2x) Put x = 675° tan 675° = sin 135°/ 1 cos 135° Now sin 135° =Cos^2x(1tan^2x)=1 secxtanx(1sin^2x)=sinx cos^2(2x)sin^2=0 ** cos^2x(1tan^2x)=1 cos^2xsin^2x/cos^2x=1 cos^2xsin^2x=1 left side = right side, therefore, equation is an identity secxtanx(1sin^2x)=sinx (1/cosx*sinx/cosx)(11cos^2x (sinx/cos^2x)(cos^2x)=sinx left side = right side, therefore, equation is an identity cos^2(2x)sin^2=0 cos^2xsin^2xsin^2x




Solved Question 1 Prove The Following Trigonometric Identities Sin2i Cos2i 1 2 Cos2i Tan2i 1 1cos2i Sini Tani Cosi 1cosi Tan2xsin2x 1 Tan2x Cos2x 1 Tan2x 1 Sinx1 Tanx Tanxsinx Cosx Sinx Cosxsinx Cosx Sin4x Cos4x Tanx Cotxtan2x Cot2x




Solved Let Tan 2x 1 2tan 2 Y Then Prove That Cos 2y 1 2cos 2x
Prove that 1cosx/1cosx=tan^2x/2 dai so chung minh dang thuc (1Sin2x)/Cos2x=Tan(pi/4x) Trigonometry Simplify the expression using trig identities 1 (sin4x cos4x)/(sin2x cos2x) 2 (sinx(cotx)cosx)/(2cotx) Trigonometry How do you verify the equation is an identity?Integrating Al and Bl wrt x, We have A — sin 2x— log ( sec 2x tan 2N )CI B — cos2x Hence complete solution is y— cos 2x c2 sin2x — cos 2x log (sec 2x tan 2x) Ans EM52 Q14 Solve d2y dy 3 v2 dv BTech (11 serm) Hence the given equation is not exact therefore to use an integration factor here to change the given' h intoProve the identity 1 cos (2x)/sin (2x) = tan (x) 1 cos (2x)/sin (2x) = 1 (1 2sin^2 (x))/2 sin (x) () = 2 ()^2/2sin (x)cos (x) = tan (x)




Solved Proving Trigonometric Identities Q1 Prove That Sin 2x Chegg Com




Prove That Cos2x 1 Tan 2x 1 Tan 2x Youtube
Answer (1 of 5) {2/(1cos x)} tan^2(x/2)=1 LHS =2/{12cos^2(x/2)1}tan^2(x/2) = 2/2cos^2(x/2) tan^2(x/2) =1/cos^2(x/2) sin^2(x/2)/cos^2(x/2) ={1 sin^2(x/2)}/cos^2(x/2) =cos^2(x/2) / cos^2(x/2) = 1Math Trigonometry Trigonometry questions and answers 1 Find sin 2x, cos 2x, and tan 2x if sin x= and x terminates in quadrant I 15 0/6 sin 2x = 0 x 5 ?Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Solved For 1 Through 4 Prove The Following Identities 1 Chegg Com



1
Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers byCos 2x 1 tan 2x 1 cos 2x 1 tan 2x 1 (1cosx)/(1cosx) * (1cosx)/(1cosx) = (1cosx)^2 / (1 cos^2x) = (1cosx)^2/sin^2x = ((1cosx)/sinx)^2 = tan^2 x/2 from your halfangle formulas



How Would You Evaluate Lim X Tending To P 4 1 Tan X Cos 2x Using L Hospital S Rule Quora




Solved Prove An Identity By Using Double Angle Identities Chegg Com
Prove as an identity; Multiply the left side in the numerator and denominator by 1tanx and simplify to get the answer ##(1tanx)^2 / (1tan^2 x)## =##(1tan^2x 2tanx)/(1 (sin^2x/cos^2x)##Cos 2x tan 2x 0




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube
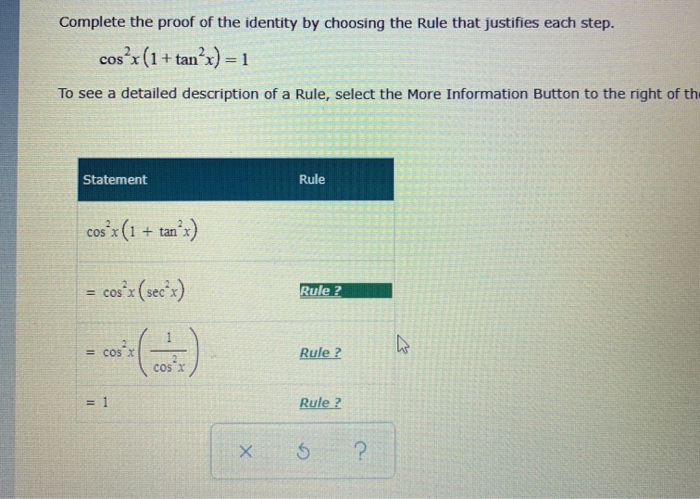



Solved Complete The Proof Of The Identity By Choosing The Chegg Com
Given,cos2x cos4x = 1cos4x = 1 cos2xcos4x = sin2xcos2x cos2x= sin2x Given,cos2x cos4x = 1cos4x = 1 cos2xcos4x = sin2xcos2x cos2x= sin2x Previous Year Papers Download Solved Question Papers Free for Offline Practice and view Solutions Online If cos 2 x cos 4 x = 1, then tan 2 x tan 4 x = ?Q Solve the following trig equations 2 sec2 x tan2 x − 3 = 0 sec x tan x = 1 2 cos2 x2 −√2 = 0 A Consider the equation 2sec2xtan2x3=013sec2x2sec2x=043sec2x=0secx=233, secx=233x=π62πn, x= We have to prove $$\frac{1}{\tan(x)(1\cos(2x))}=\csc(2x)=\frac{1}{\sin(2x)}$$ Multiply both sides by $\tan(x)$ and apply $\sin(2x)=2\sin(x)\cos(x)$ and you arrive at




Tan X 2 1 Cos 2x 1 Cos 2x Youtube




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube
Prove \cot(2x)=\frac{1\tan^2(x)}{2\tan(x)} en Related Symbolab blog posts High School Math Solutions – Trigonometry Calculator, Trig Identities In a previous post, we talked about trig simplification Trig identities are very similar to this concept An identity Prove that the equation Is an identity Sec^4x Tan^4x = Sec^2x Tan^2x math use the quotient and reciprocal identities to simplify the given expression cot t sin t csc t sin t tan t cot t cot t sec t math prove that 1cos2x÷1cos2x=tan^2x 'Show that `tan^2 x = (1 cos(2x))/(1 cos(2x))`'tan^2x=1cos2x/1cos2x true or false1cos2x/1cos2x is equal to1cos2x/1
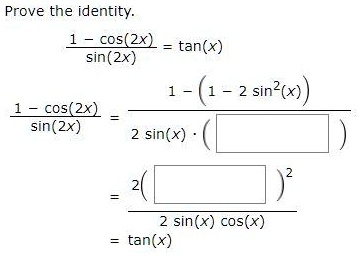



Solved Prove The Identity Cos 2x Tan X Sin 2x 1 1 2 Sin X Cos 2x Sin 2x 2 Sin X 2 Sin X Cos X Tan X




8 Prove That Cos2x 1 Tan 2x 1 Tan 2x Brainly In
prove that cot x tan 2x1 =sec 2x Trigonometry How do you verify the equation is an identity?Answer (1 of 3) I think you must have typed this wrongly I suspect you meant this Best answer Let us consider the LHS cos 2x/ (1 sin 2x) As we know that, cos 2x = cos2 x – sin2 x Sin 2x = 2 sin x cos x Therefore, On multiplying numerator and denominator by



How Do You Verify Cos 2x Sin 2x 1 Cos 2x Csc 2x Socratic




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
Click here👆to get an answer to your question ️ Prove that cos 2x = 1 tan^2x1 tan^2xI need to use the fact that $\tan 2x=\sin2x \ /\cos2x$ to prove that $$\tan 2x=\frac{2\tan x}{1\tan^2x}$$ I don't know where to start Please help or hint Thanks in advanceTanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac {\cos ^2 x} {1\tan x}




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




Analytic Trig Ppt Video Online Download
Sin (2x) = (2tan (x)) / (1tan^2 (x)) *** Start with RHS 2tanx/ (1tan^2x) 2tanx/ (sec^2x) 2 (sinx/cosx)/ (1/cos^2x) 2sinxcosx=sin2xYes, if the term at the bottom is tan^2 x, you typed tan^x, and I read it as tan x I got the proof, give me a bit of time to type it I'm sorry Mr Reiny you are right it is tan^2x LS= 2tanx/(1tan^2x) 1/(2cos^2x 1) = 2sinx/cosx 1/(1sin^2x/cos^2x) 1/(2cos^2x (sin^2x cos^2x)) Get an answer for 'Prove that tan^2x/(1tan^2x) = sin^2x' and find homework help for other Math questions at eNotes




Prove Sinx Cosx Tanx 1 Cos 2x Youtube




いろいろ Tan2x 1sec2x ただの悪魔の画像
Solution Let us start with LHS 2tanx 1tan2x 2 t a n x 1 t a n 2 x 1 tan 2 x = sec 2 x tan x = sin x/cos x ⇒ 2s i nx cosx sec2x 2 s i n x c o s x s e c 2 x ⇒ 2s Ex 33, 23 Prove that tan4𝑥 = (4 tan〖𝑥 (1−tan2𝑥)〗)/(1 − 6 tan2 𝑥tan4 𝑥) Taking LHS tan 4x We know that tan 2x = (2 𝑡𝑎𝑛𝑥)/(1 − 𝑡𝑎𝑛2 𝑥) Replacing x with 2x tan (2 × 2x) = (2 𝑡𝑎𝑛2𝑥)/(1 − 𝑡𝑎𝑛2 2𝑥) tan 4x = (2 𝑡𝑎𝑛2𝑥)/(1 − 𝑡𝑎𝑛2 2𝑥) = (2 ta(1cosx) / (1cosx) =tan^2(x/2) x/2 =y → x=2y The question becomes (1cos2y) / (1cos2y) =tan^2(y) so (1cos2y) / (1cos2y)= =(1–(1–2(siny)^2))/(12(cosy)^2–1) =(2(siny)^2)/(2(cosy)^2) =(siny/cosy)^2 = (tany)^2 if you do not like to use "y" , th




Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube




Solved Prove The Following Identities 1 Sin 2x Cos 2x Chegg Com
Recall the formula tanA = sinA/cosA sin2A = 2sinAcosA cos2A = cos^2Asin^2A sinA = 1/cscA Left hand side =1/tanx(1cos2x) = 1/(sinx/cosx)(1cos^2xsin^2x) = 1/(sinx/cosx(cos^2xcos^2x)) = 1/(sinx/cosx(2cos^2x) = 1/2sinxcosx = 1/sin2x = Get an answer for 'verify (1 tan^2x)/(tan^2x) = csc^2x' and find homework help for other Math questions at eNotes Just mess around with the left hand side a bit $$(1\cos^2 x)(1\tan^2 x)$$ We know the following identity $$1\cos ^2 x = \sin^2 x$$ Now, simply replace $1\cos^2 x$ with $\sin^2 x$ $$(\sin^2 x)\cdot(1\tan^2 x)$$ $$\sin^2 x\sin^2 x\cdot\tan^2 x$$ $$\sin^2 x\sin^2 x\cdot\big(\frac{\sin^2 x}{\cos^2 x}\big)$$ $$\sin^2 x \frac{\sin^4 x}{\cos^2 x}$$ Now, just



Answered Prove The Following Identity 1 Tan X Bartleby




Tan2x ただの悪魔の画像
Tan^2 x = 1 cos2x/ 1 cos 2x andrianartic9331 andrianartic9331 Mathematics College answered • expert verified True or false Tan^2 x = 1 cos2x/ 1 cos 2x 2 See answers Advertisement I'm currently stumped on proving the trig identity below $\tan(2x)\tan (x)=\frac{\tan (x)}{\cos(2x)}$ Or, alternatively written as $\tan(2x)\tan (x)=\tan (x)\sec0 1 2tan 2 x 2tan 4 x B 1




Cos2x 1 Sin2x Tan Pi 4 X Double And Half Angle Identity Youtube




Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube
Answer to Find sin(2x), cos(2x), and tan(2x) from the givenTan^2xtan^2y=sec^2xsec^2y and, how do you factor and simplify, cscx(sin^2xcos^2xtanx)/sinxcosx Math Prove the identity sec^4x tan^4x = 12tan^2xAnswer \dfrac{\csc^2\,x}{1 \tan^2\,x} = \cot^2\,x \text{Left hand side} \dfrac{\csc^2\,x}{1 \tan^2\,x} =\dfrac{\csc^2\,x}{\sec^2\,x} =\dfrac{\cos^2\,x}{\sin^2\,x




Proof Cos 2x 1 Tan 2x 1 Tan 2x Youtube
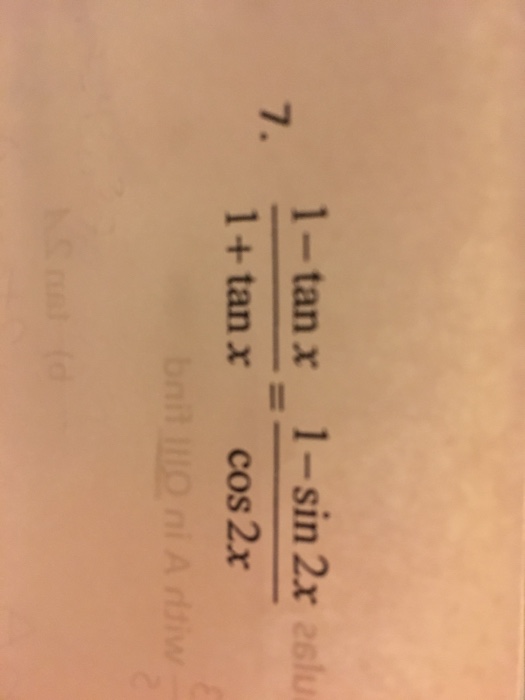



Solved 1 Tan X 1 Tan X 1 Sin 2x Cos 2x Chegg Com
tan(2x) To prove tan(2x) = (2 tan x) / (1 – tan²x) Proof First let us start from LHS tan(2x) We know that tan x = sin x / cos x sin(2x) / cos(2x) We know that sin 2A = 2 sin A cos A 2 sin x cos x / cos(2x) Also cos 2A = cos²A – sin²A 2 sin x cos x / (cos²x – sin²x) = Divide the numerator and denominator by cos²x



Tan2x ただの悪魔の画像
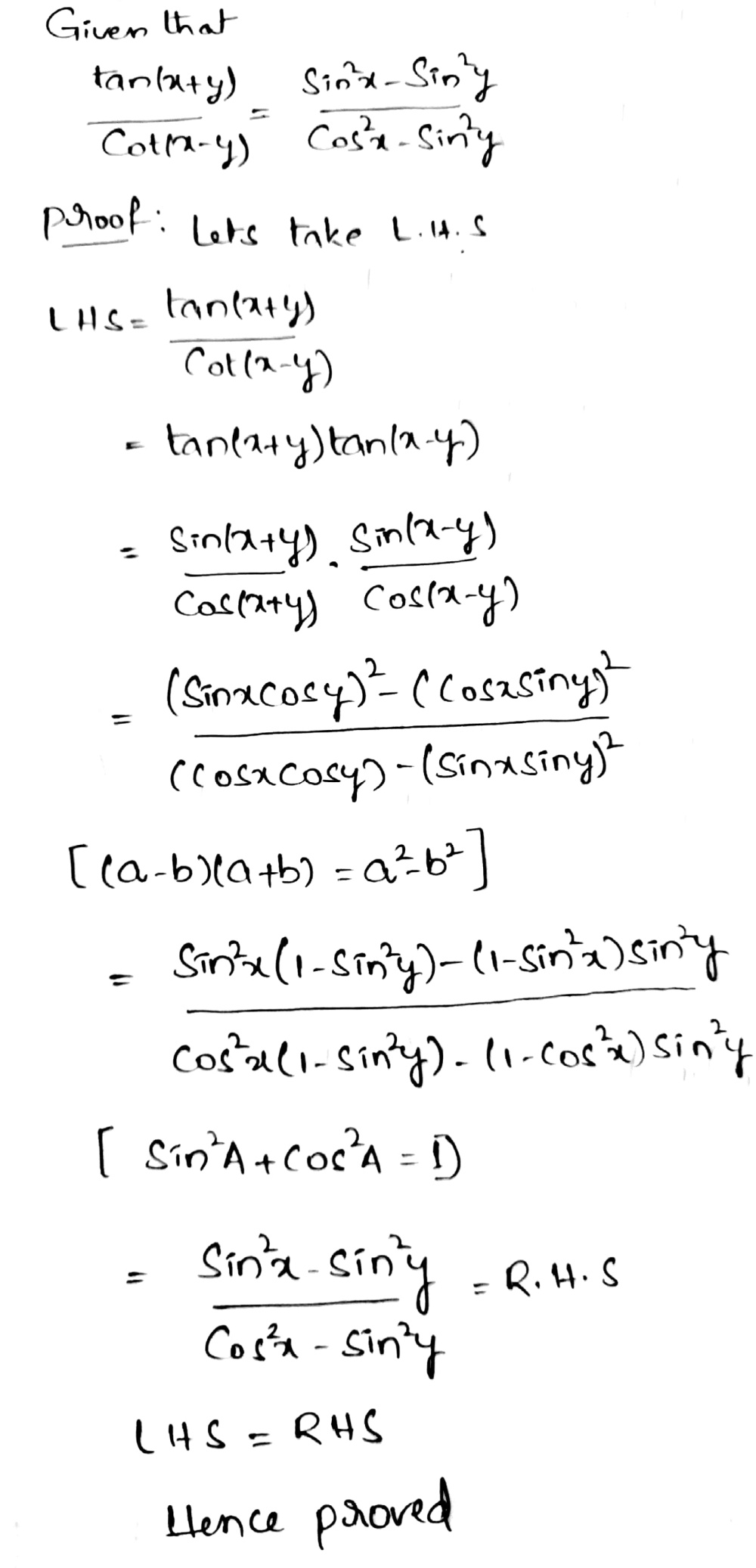



Prove Each Of The Following Frac Tan X Y Cot X Y Frac Sin 2x Sin 2y Cos 2x Sin 2y Frac Tan 2x Tan 2y 1 Tan 2xtan 2y Snapsolve




How Do You Prove Tan 2x Secx 1 1 Secx Socratic



Prove Sin2x 2tanx 1 Tan 2x Socratic




Prove That Sin 2x 1 Cos 2x Tan X Brainly In




Prove That Tan3xtanx 2cos2x 12cos2x 1




Cos 2x Formula Derivation Examples What Is Cos 2a Formula



Prove The Identity Cos 2x 1 Sin 2x Tan P 4 X Sarthaks Econnect Largest Online Education Community




Verify Identity Tan 2 X 1 Tan X Sec X 1 Sin X Cos 2 X Youtube
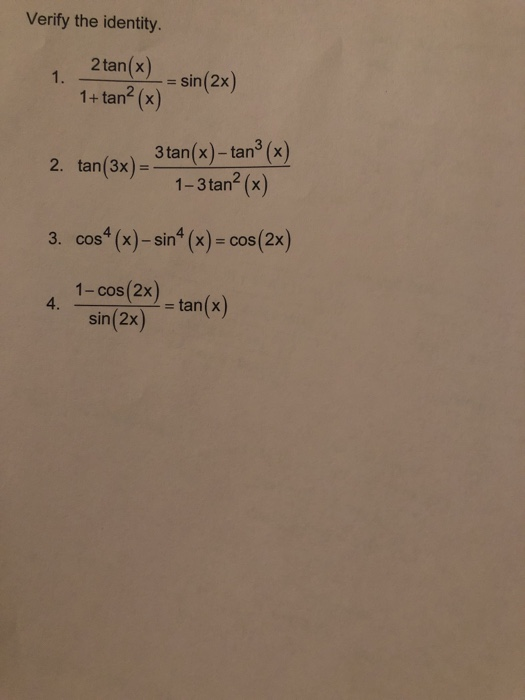



Solved Verify The Identity 2tan X Sin 2x 1 Tan2 X 2 Chegg Com
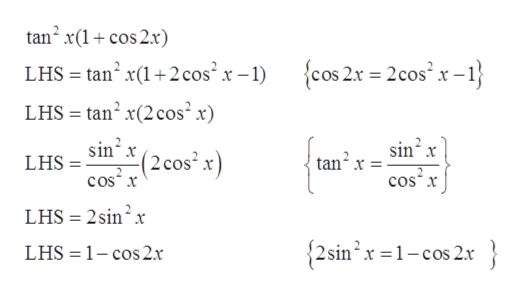



Answered Tan2x 1 Cos2x 1 Cos2x Verify The Bartleby




Ch 7 Trigonometric Identities And Equations Ppt Video Online Download
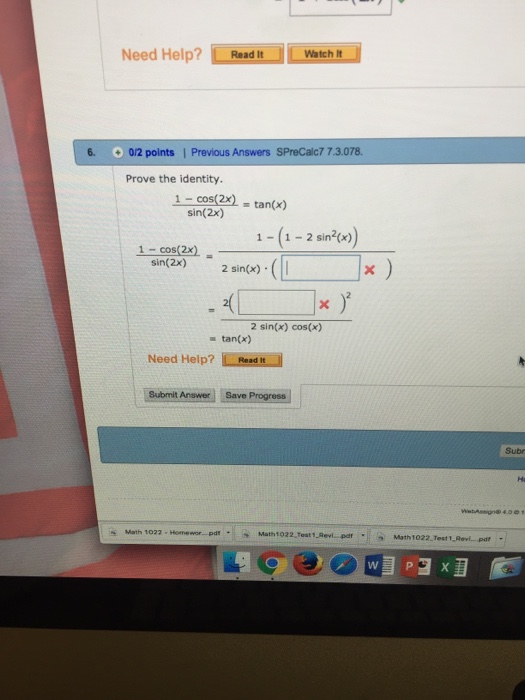



Solved Prove The Identity 1 Cos 2x Sin 2x Tan X 1 Chegg Com



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




Trigonometric Identity 1 Cos2x Sin2x 1 Cos2x Sin2x Tanx Youtube



Prove The Identity Cos 2x 1 Sin 2x Tan P 4 X Sarthaks Econnect Largest Online Education Community




Prove That Sec8x 1 Sec4x 1 Tan8x Tan2x Maths Trigonometric Functions Meritnation Com




Prove That 1 Sin 2x Cos 2x 1 Sin 2x Cos 2x Tan X Youtube




1 Tan 1 Sin 2 Prove 1 Tan Cos 2 Start With 1 Tan 1 Tan Sin Cos Sin




Sin2x Cos2x 1 Proof




Trigonometric Identity 1 Cos2x Sin2x 1 Cos2x Sin2x Tanx Youtube



1




If Cos 2x 1 Cos 2x 1 Tan 2 2y 3 Sin3z 4 Then X Is




Solved 1 Prove That Cos 2x 2 Cos X 1 2 Prove That Chegg Com



1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit



Prove The Identity Sin X Sin 2x 1 Cos X Cos 2x Tan X Sarthaks Econnect Largest Online Education Community




Piu Veloce Sin2x Cos2x 1
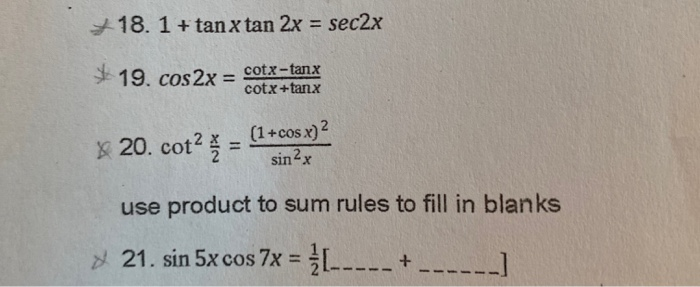



Solved 18 1 Tan X Tan 2x Sec2x 19 Cos2x Cotx Tank Chegg Com




1 Tan 2x 1 Tan 2x 2 Cos 2x 1 Brainly In



Solved Explian The Proof For This Tan 2x 1 Tan X Co5 2x Solution Starting With The Left Side Sin 2x Sm X Step 1 Cos 2x Cos X Sin 2x Course Hero




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




How Do You Prove That Tanx Secx 1 Tanx Secx 1 1 Sinx Cosx Socratic



How To Prove That 1 Sin 2x 1 Cotx Cos 2x 1 Tanx Sinxcosx Using Trig Identities Quora




Answered Prove The Following Identity 1 Tan X Bartleby



1 Tan 2x Sec 2x



Prove That Cos2x Cos 2x Sin 2x 2cos 2x 1 1 2sin 2x 1 Tan 2x 1 Tan 2x Sarthaks Econnect Largest Online Education Community




Solved Prove That The Equations Are Identities 1 Chegg Com




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com



A 1 Tan X Tan X 1 Show That A Ta 1 Cos 2x Sin 2x Sin 2x Cos 2x Sarthaks Econnect Largest Online Education Community
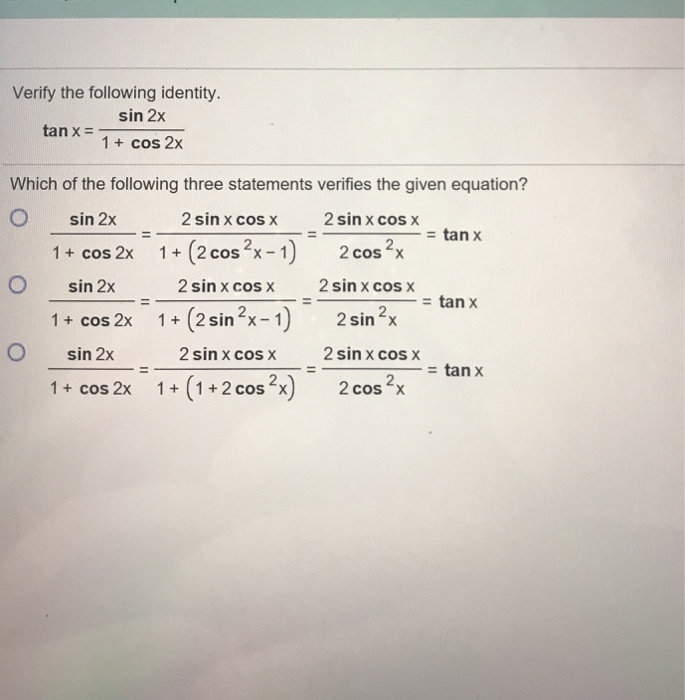



Solved Verify The Following Identity Tan X Sin2x 1 Cos Chegg Com




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




Solved Verify That The Equation Is An Identity Tan 2x Cot Chegg Com



Tan2x ただの悪魔の画像
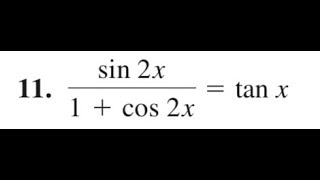



Verify Sin 2x 1 Cos 2x Tan X Youtube



1
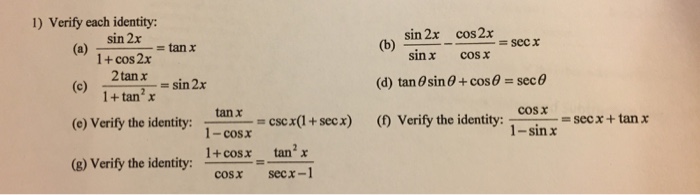



Solved Verify Each Identity A Sin 2x 1 Cos 2x Tan X Chegg Com




Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube



How To Prove Math Dfrac Sqrt 1 Cos 2x 1 Cos 2x Tan X Math Quora
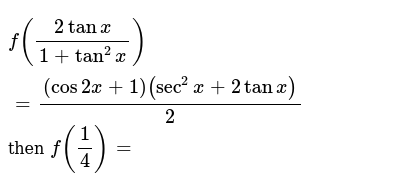



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2 Then F 1




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
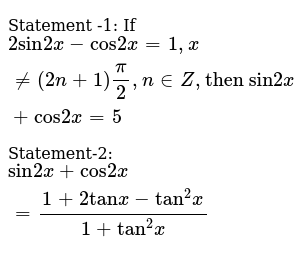



Find Sin 2x Cos 2x And Tan 2x From The Given Information Tan X




Trigonometric Identity Sinx Sin2x 1 Cosx Cos2x Tanx With Double Angle Expressions Youtube



How To Simplify Sin 2x 1 Cos 2x To Cot X Quora
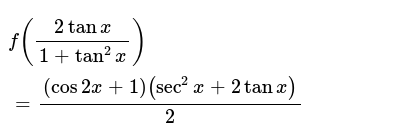



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2
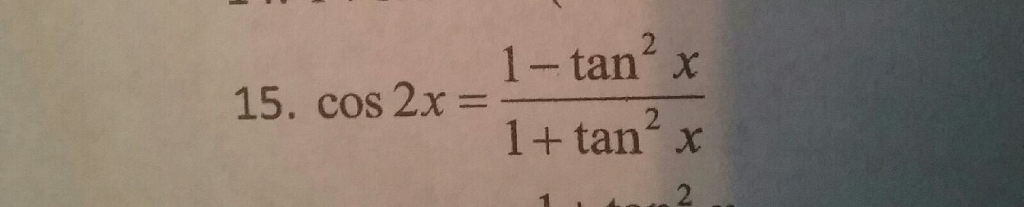



Solved Prove The Identity Cos 2x 1 Tan 2 X 1 Tan 2 X Chegg Com



bestpictjcry Tan 2x Tan 2x
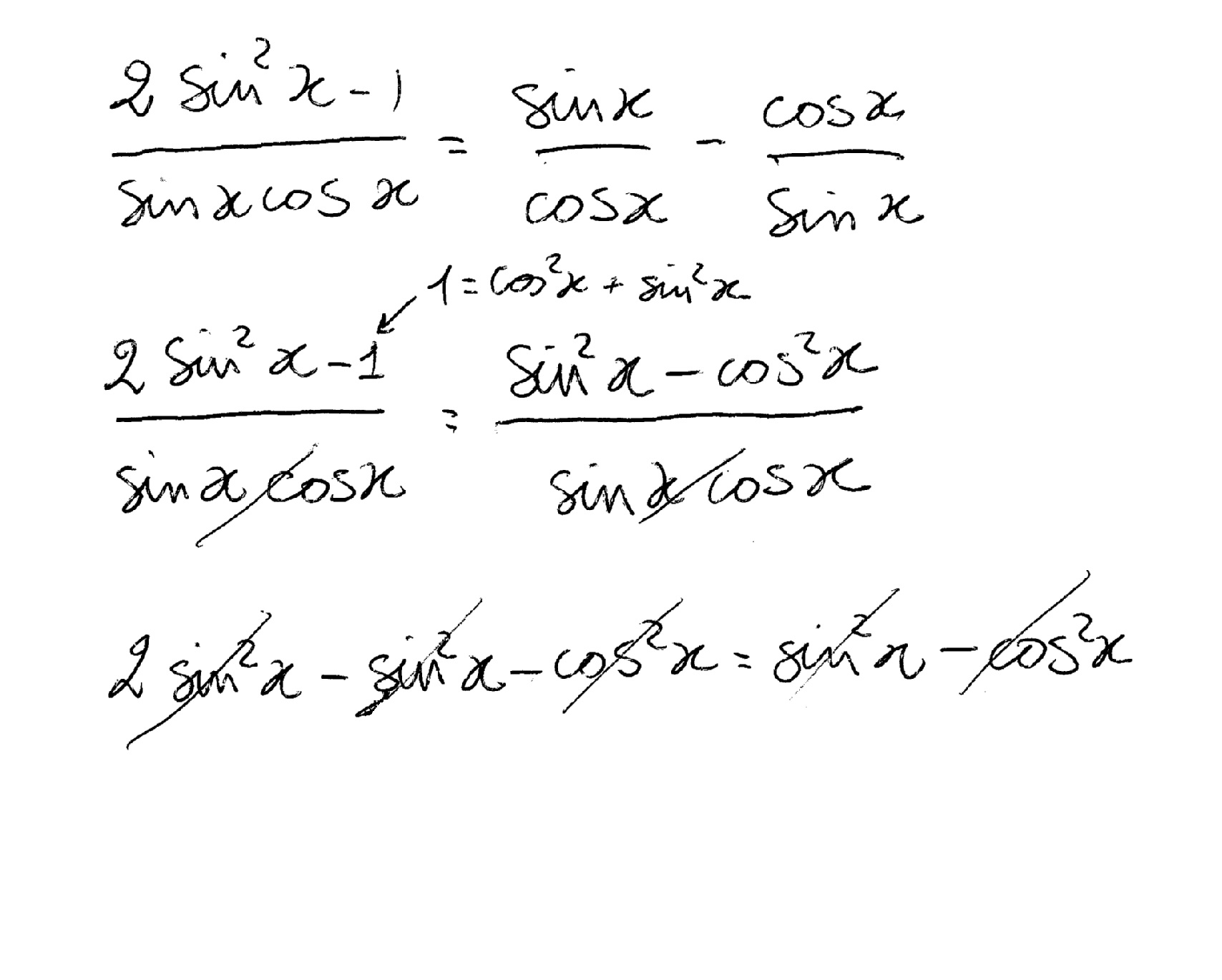



How Do You Prove 2sin 2x 1 Sinxcosx Tanx Cotx Socratic




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic




Prove The Identity 1 Tan 2x 1 Tan 2x 1 2sin 2x In Urdu Hindi Youtube




Prove That 1 Sin 2x Cos 2x 1 Sin 2x Cos 2x Tan X
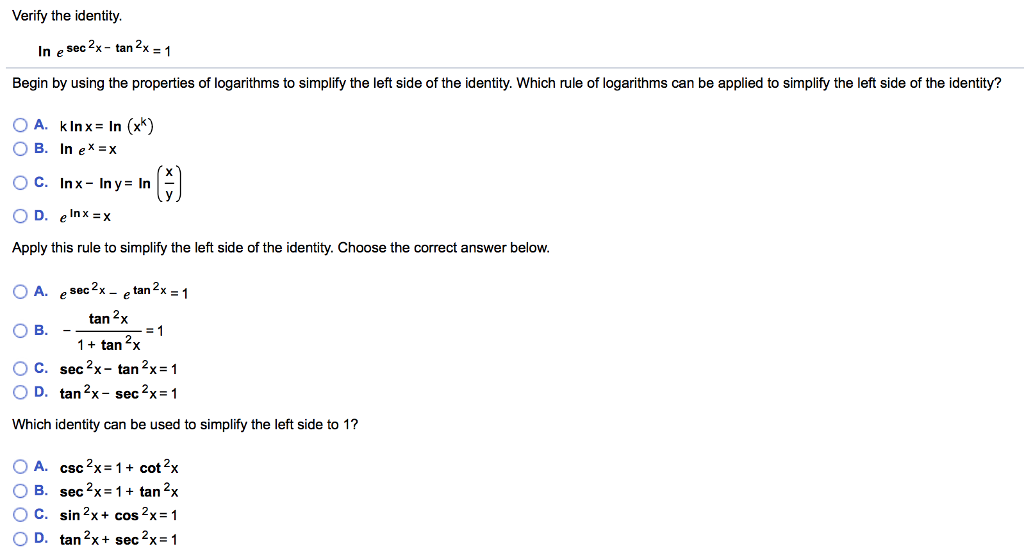



上 Tan2x Identity ただの悪魔の画像




いろいろ Tan2x 1sec2x ただの悪魔の画像



Solved Prove The Identity Cos 2x 1 Tan 2x 1 Note That Chegg Com



What Is The Formula Of 1 Cos2x Quora
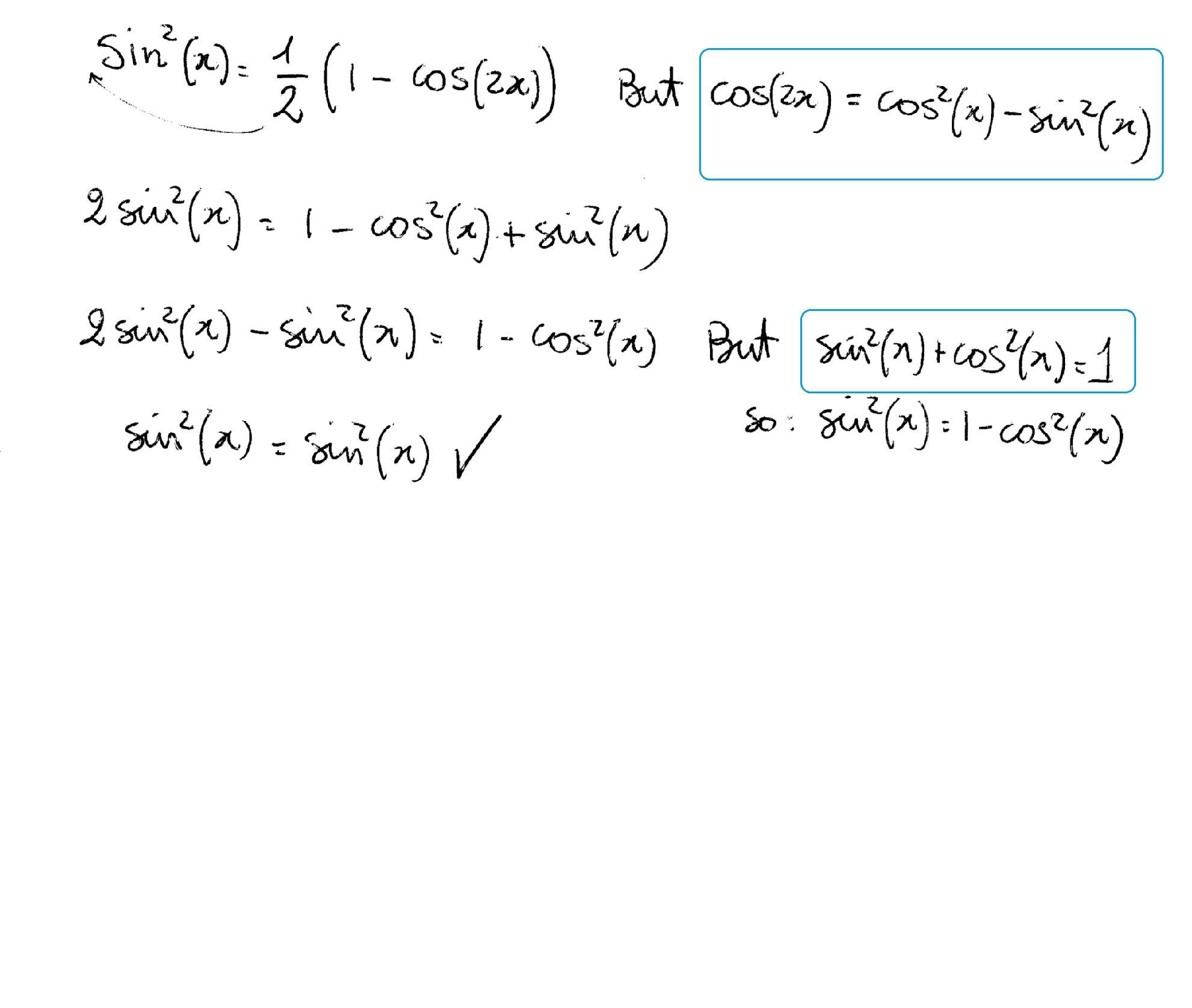



How Do You Verify Sin 2 X 1 2 1 Cos2x Socratic
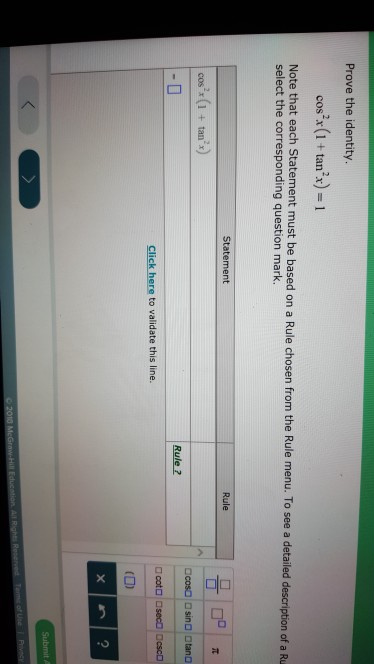



Solved Prove The Identity Cos 2x 1 Tan 2x 1 Note That Chegg Com
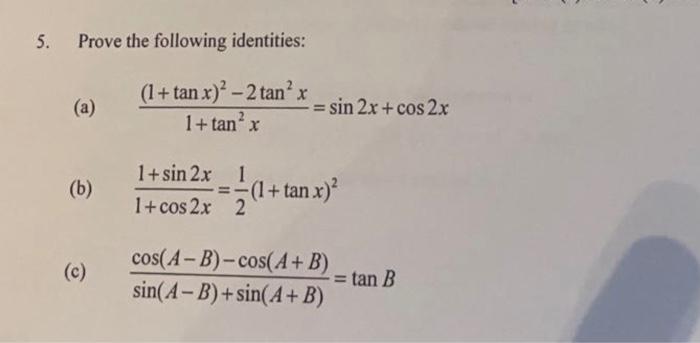



Solved 5 Prove The Following Identities A 1 Tan X 2 Chegg Com




Prove That 1 Sin2x Cos2x Sin2x Cos2x Tanx Maths Meritnation Com




Solved 1 Sin 2 0 Cos 2x 1 Tan 3 To Prove That 1 Tan 2 Chegg Com
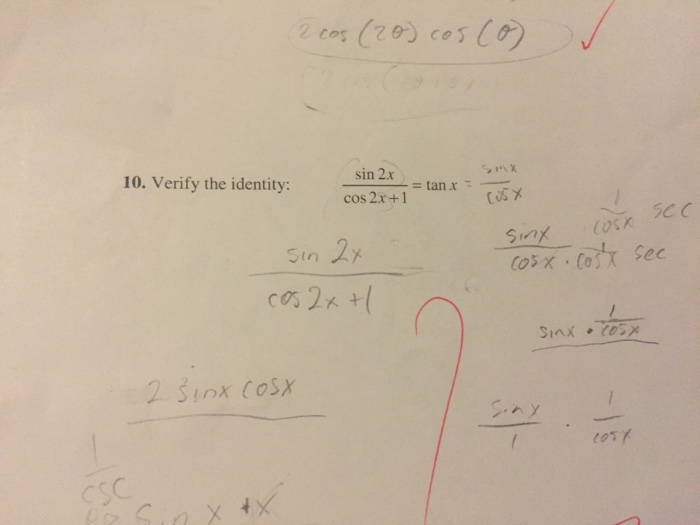



Solved Verify The Identity Sin 2x Cos 2x 1 Tan X Chegg Com




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube
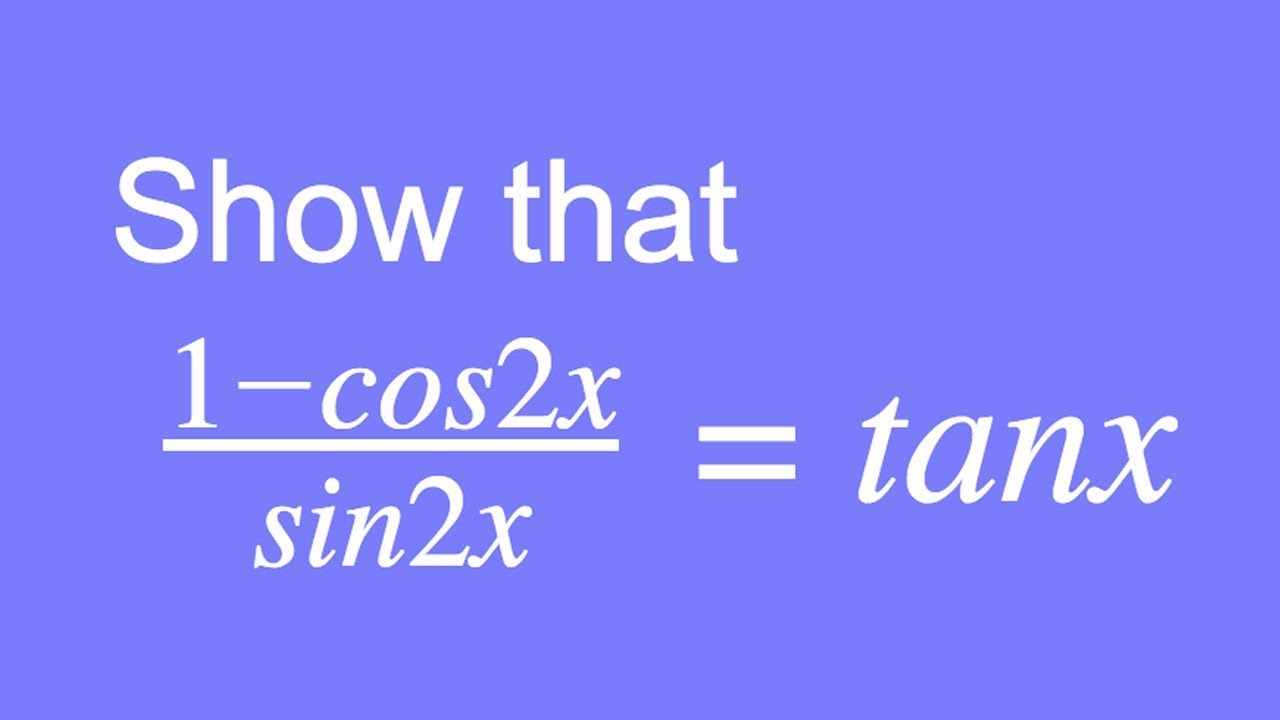



How To Show That 1 Cos2x Sin2x Tanx Youtube




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
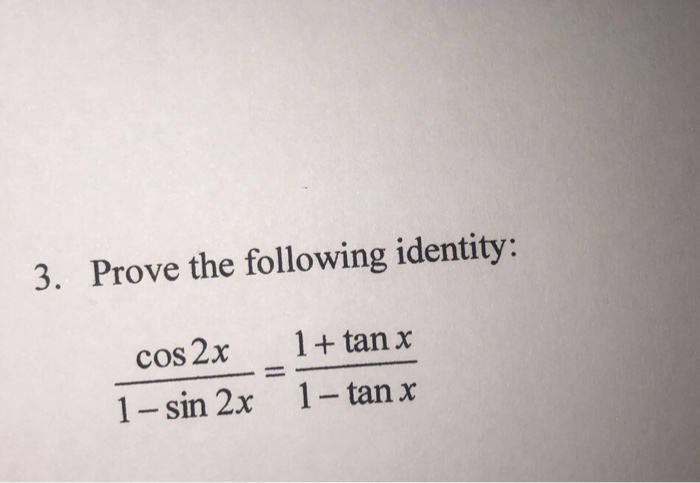



Solved 3 Prove The Following Identity Cos 2x 1 Sin 2x Chegg Com
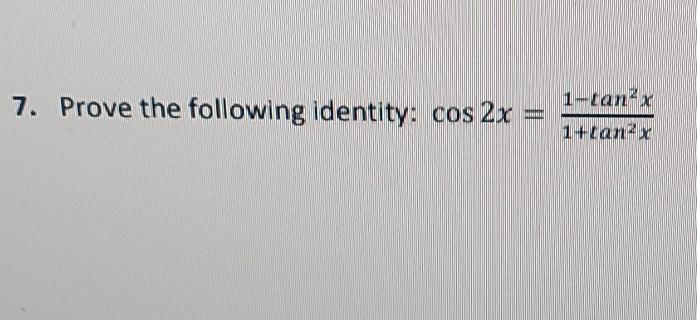



Solved 7 Prove The Following Identity Cos 2x 1 Tan2x Chegg Com



0 件のコメント:
コメントを投稿